This is part 3 of a 3 part series on KZG Commitments. Here are links to part 1, part 2 and the summary article.

KZG Commitments Part 2: Open

Prerequisites

Elliptic Curve Cryptography

Elliptic curve cryptography looks unapproachable, but it's totally understandable with a decent amount of high school algebra. 

Check out this Into to Elliptic Curve Cryptography and you'll have the math you need to get through this article.

KZG Commitment Scheme

Deep Dive: Polynomial Commitment Schemes

A polynomial commitment scheme allows one party to publicly commit to a specific dataset without giving away any info about the underlying data. 

Once a commitment has been calculated, the data is locked in; any changes to the data will result in invalid proof generation.

A KZG polynomial commit can be "opened" with any data point without revealing the entire dataset. 

Let's say I am thinking of 10 words. I write them each down on different pieces of paper. If you guess correct, i ONLY show you the correct 1 (keeping the other 9 hidden).

KZG Commitments Part 1: Commit

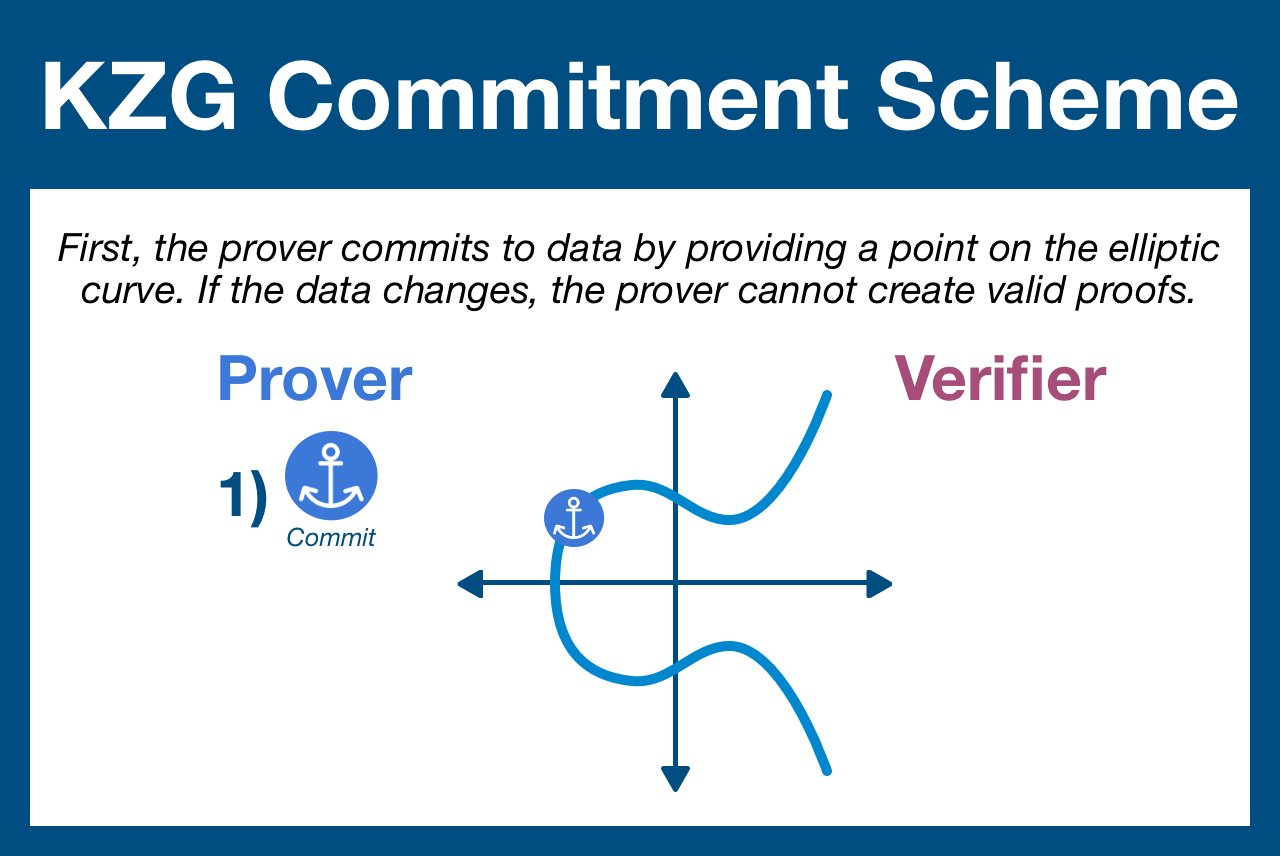
Deep Dive: KZG Commitments Part 1 - Commit

First, we generate a polynomial from our data using a mathematical process called a Lagrange Interpolation. 

Then, we calculate the value of this polynomial evaluated with a secret number S (hidden within an elliptic curve).

Once the commitment is calculated, the prover is bound to this specific data. The scheme is going to pivot around this specific value, derived from this specific polynomial. 

A change to even a single bit will result in a brand new polynomial (and therefore commit value).

KZG Commitments Part 2: Open

Deep Dive: KZG Commitments Part 2 - Open

The verifier (the party challenging the prover) knows at least one piece of data in the committed data set, and so requests a proof around data point z. The prover calculates [h(S)] and f(z), returning the values to the verifier.

Just like our original commitment is simply f(x) evaluated through the elliptic curve at S, our proof is going to be an evaluation of h(x) at S... ALSO an elliptic curve point! 

The question: how can we use our f(S), f(z), h(S) and z to prove our prover is being honest?

Verifying the Quotient Polynomial

The core of KZG commitment is this "h(x)" polynomial. If the prover is honest and is still committed to the original data, this is a simple polynomial to derive and to evaluate. And so, we are simply going to test this polynomial by having the prover evaluate it at S.

Remember, the verifier may or may not have access to the full original data set and therefore the verifier cannot build the polynomial and check the provers value. Instead, we are going to check a slightly different equation:

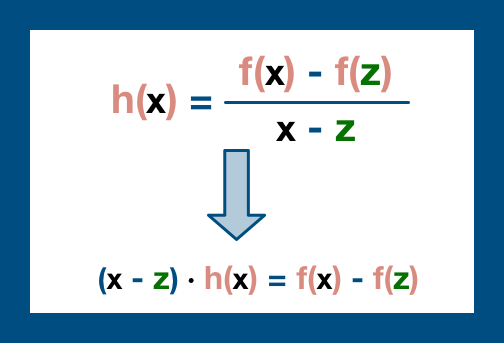
But remember, we aren't working with standard functions; we are working with elliptic curves. 

And so, we have a problem. 

We have seen that we can easily add and subtract two points on an elliptic curve, but we haven't seen multiplication.

Elliptic Curve Pairings

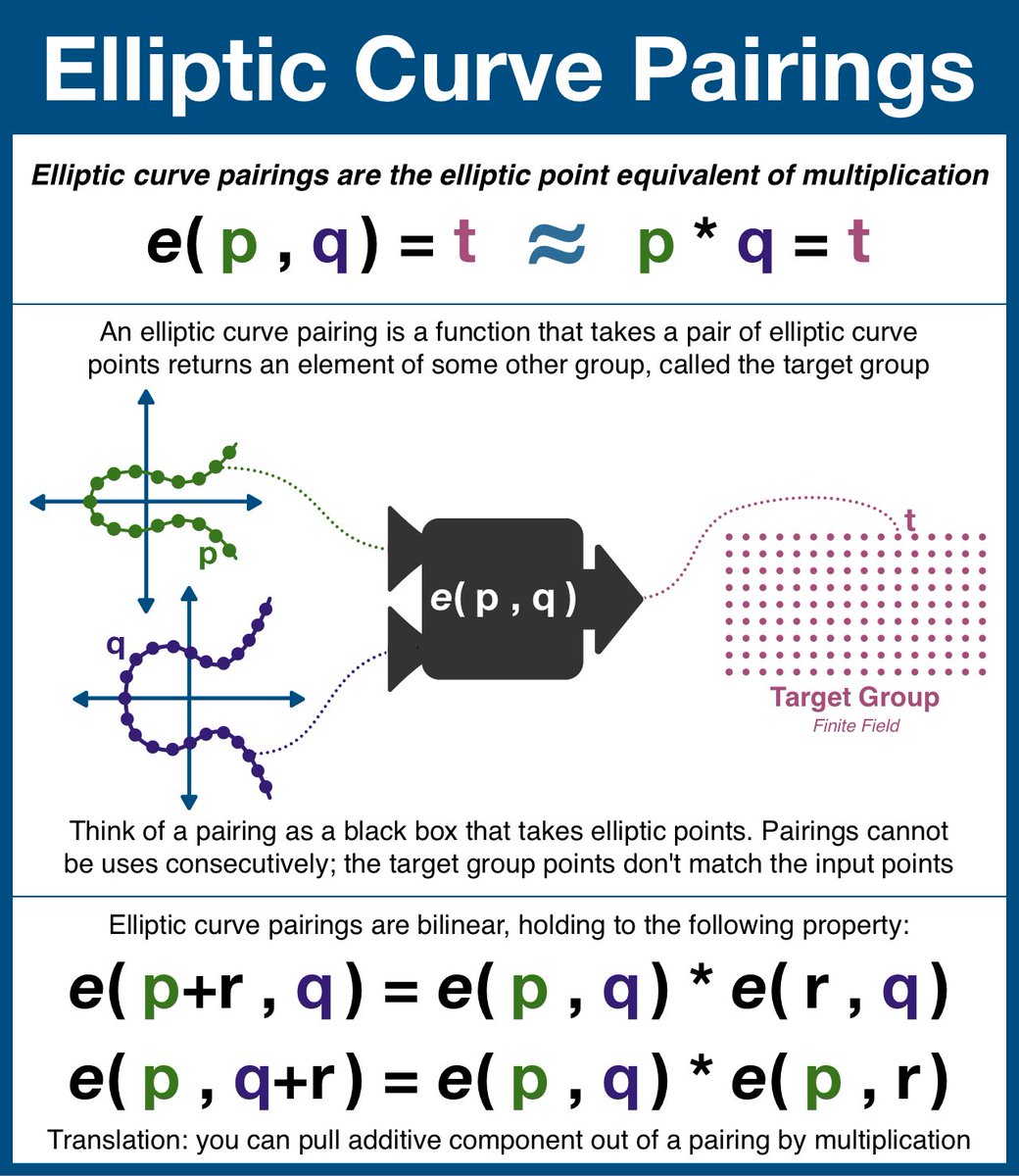
Deep Dive: Elliptic Curve Pairings

In fact, you CAN'T multiply two elliptic curve points, at least in any coherent way... not in any way that will non-destructively obscure data in the way we need. 

Fortunately, we have a solution: elliptic curve pairings.

Pairings are perhaps the most advanced math you'll ever come across. Super exciting, cutting edge research-type stuff. 

For our purposes, they are actually pretty easy: imagine pairings as the single use, irreversible version of elliptic curve point multiplication.

Verification

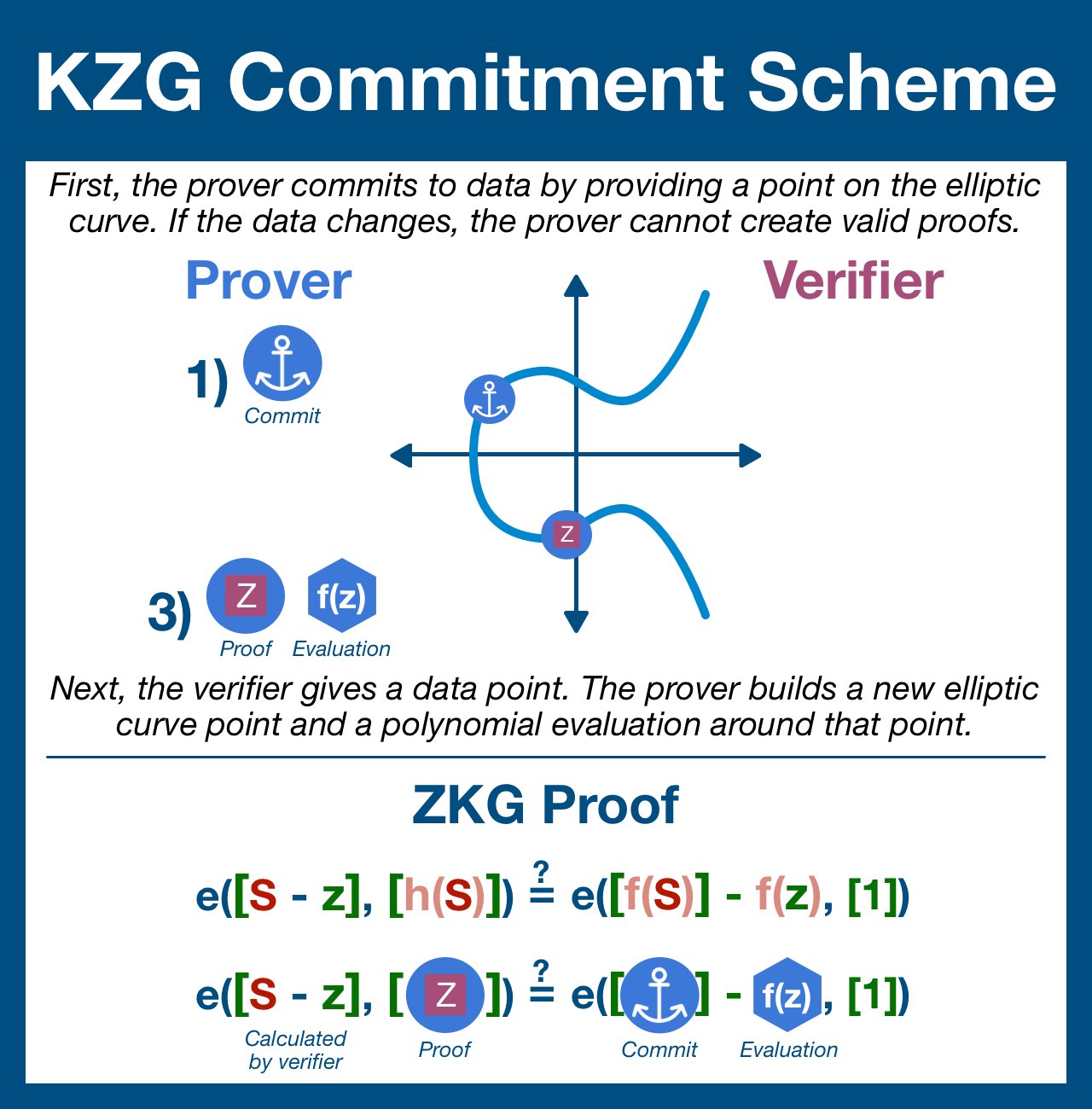
Now we have all the pieces we need to complete our KZG proof verification; let's finish creating verification conditions. 

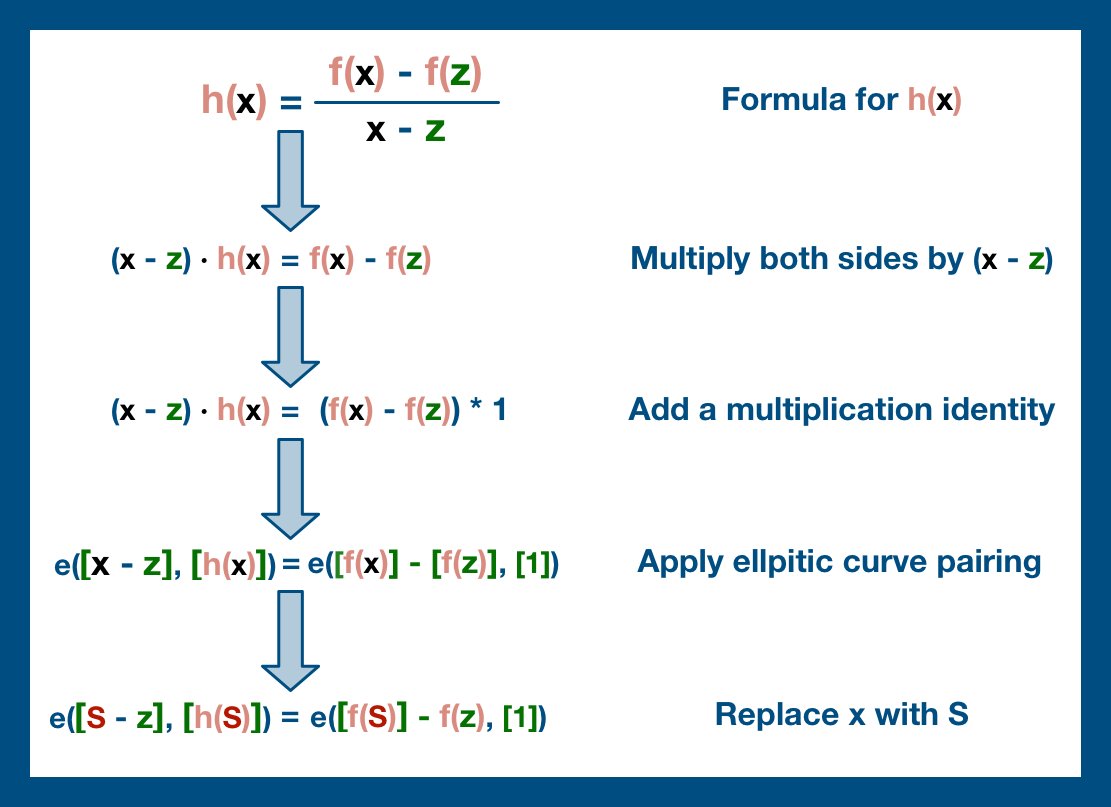
At the end of this process we will have our KZG verification expression. All we need to is evaluate each side and make sure they are equivalent.

The prover supplies 3 of 4 terms needed in the verification expression: 

• [f(S)], the commitment to the data - [h(S)]
• a commitment to h(S), where h(x) is polynomial constructed around z - f(z)
• the original polynomial evaluated at z

The verifier can calculate [S - z].

And so, the verifier computes both sides of the equation and compares the results. If the results match, then we can be mathematically certain the prover was honest! 

Need to unpack that one more time?

The purpose of the verification is to work out whether the prover successfully divided the polynomial f(x) by (x-z). If any of the data was altered, the prover wont have access to f(x). He'll be able to generate a polynomial based off the new data, but it won't verify.

Summary

Think like this: 

• Step 1: the prover committed to a dataset by creating a polynomial and evaluating it using the SRS
• Step 2: the verifier challenges the prover by giving a data point within the original data set
• Step 3: the prover comes back with two items, a curve point chosen using the prover's requested data point and an evaluation
• Step 4: the prover uses a pairing to double check that these two items were correctly calculated, using the commitment as a reference.

That's it, the entire KZG commitment scheme! 

Once the verifier has run both sides of the equation and checked for equality, the process is complete. 

We've successfully verified both the original commitment and the specific data point within the committed dataset.

Resources

Source Material - Twitter Link