
¶ Polynomial Commitments
¶ Prerequisites
¶ Hashing
Applying a hash function takes data (of arbitrary contents and size) and reduces it to a unique, compact string.
Every input produces a unique output, even if two inputs are nearly identical.
¶ Polynomial Encoding
It is possible to represent an arbitrary set of data as a polynomial; you can (relatively) quickly and easily find the equation of said polynomial through a process known as the Lagrange Interpolation.
Data → polynomial → data
Data = polynomial
¶ Public Assurance
Let's say you have a large amount of data that, for whatever reason, is private. How can you provide a public audience assurance that you will not alter the data without allowing them to see it?
The naïve option just doesn't work; we cannot just reveal all the data and allow people to publicly verify that no changes are happening.
We need to find a way to provide a unique fingerprint of that specific set of data to act as a signature.
¶ Hash-based Fingerprinting
Hash functions are a great candidate for this kind of job: a hash function irreversibly transforms an arbitrary amount of data into a unique string of uniform length. Even a single-digit change will result in an entirely new hash.
So, maybe a hash-based solution?
The problem with hash functions is that the process of creating a function's unique fingerprint necessarily destroys all other information. For example, you cannot verify if a particular piece of data was in the data set using a hash; it's all or nothing.
Once generated, a hash acts as a unique identifier, a pseudo-random string of data, and not much more.
So, we must look for alternative schemes.
¶ Polynomial Fingerprints
I encourage you to review polynomial encoding.
Let's transform our database into a polynomial, which we will refer to as f(x).
Now, we can't post f(x); that would be equivalent of posting the data.
But what if we posted a point of data on data on that polynomial; one that didn't provide a real value?
¶ A Non-Sensitive Value
Lets unpack that question.
Remember how we constructed our list of data points?
We put our data in an ordered list and one by one plotted it on a graph.
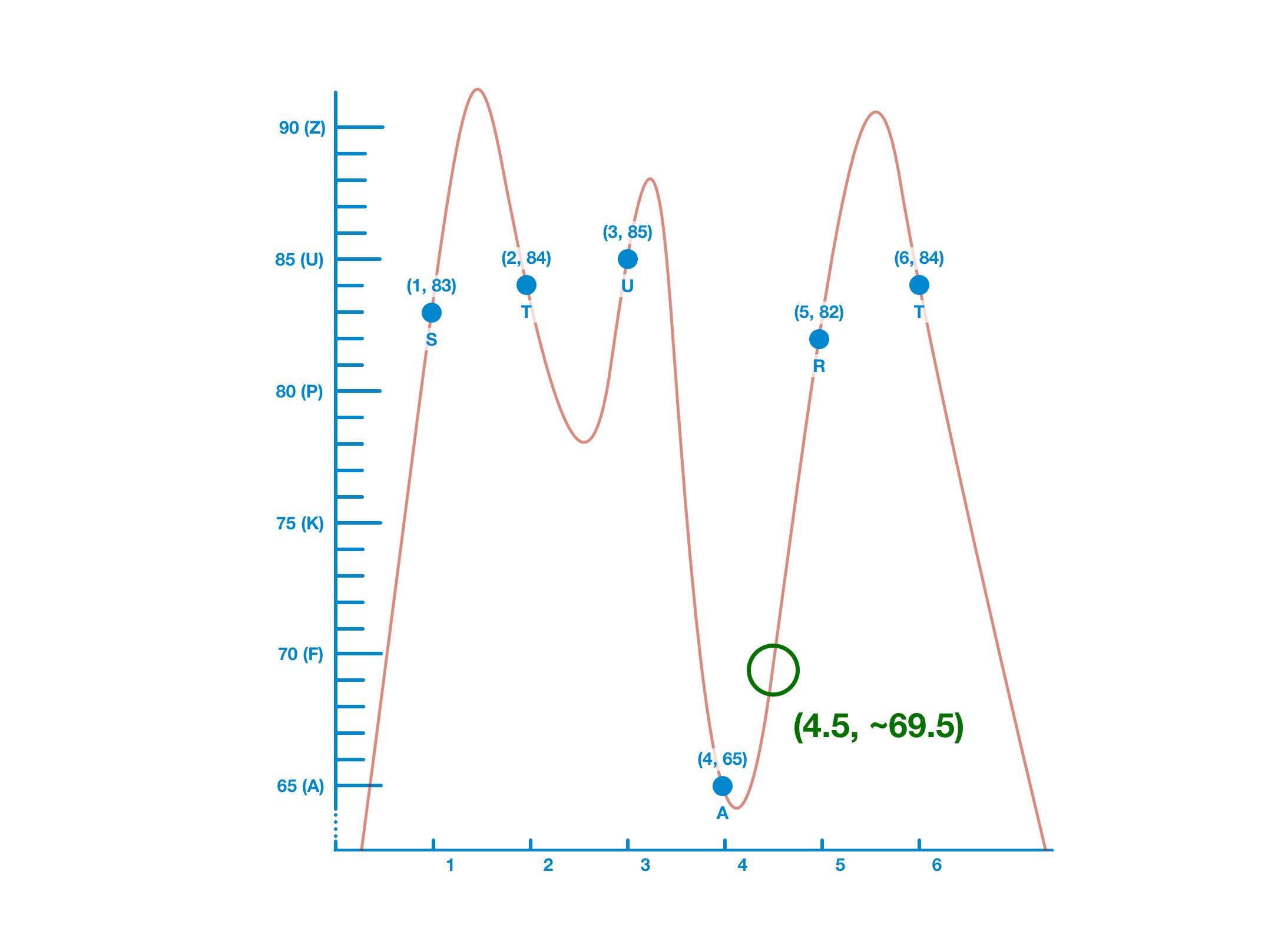
When x = 4, y = 65 - which refers to a real datapoint (A).
But when x = 4.5, y = 69.5 - which doesn't refer to real data.
So here's the idea: transform our data into a polynomial and provide the public with an evaluation value for a non-sensitive part of the curve.
Remember, the curve defined by the polynomial is infinite and your data is not; there are plenty of non-sensitive points.
¶ Commitments
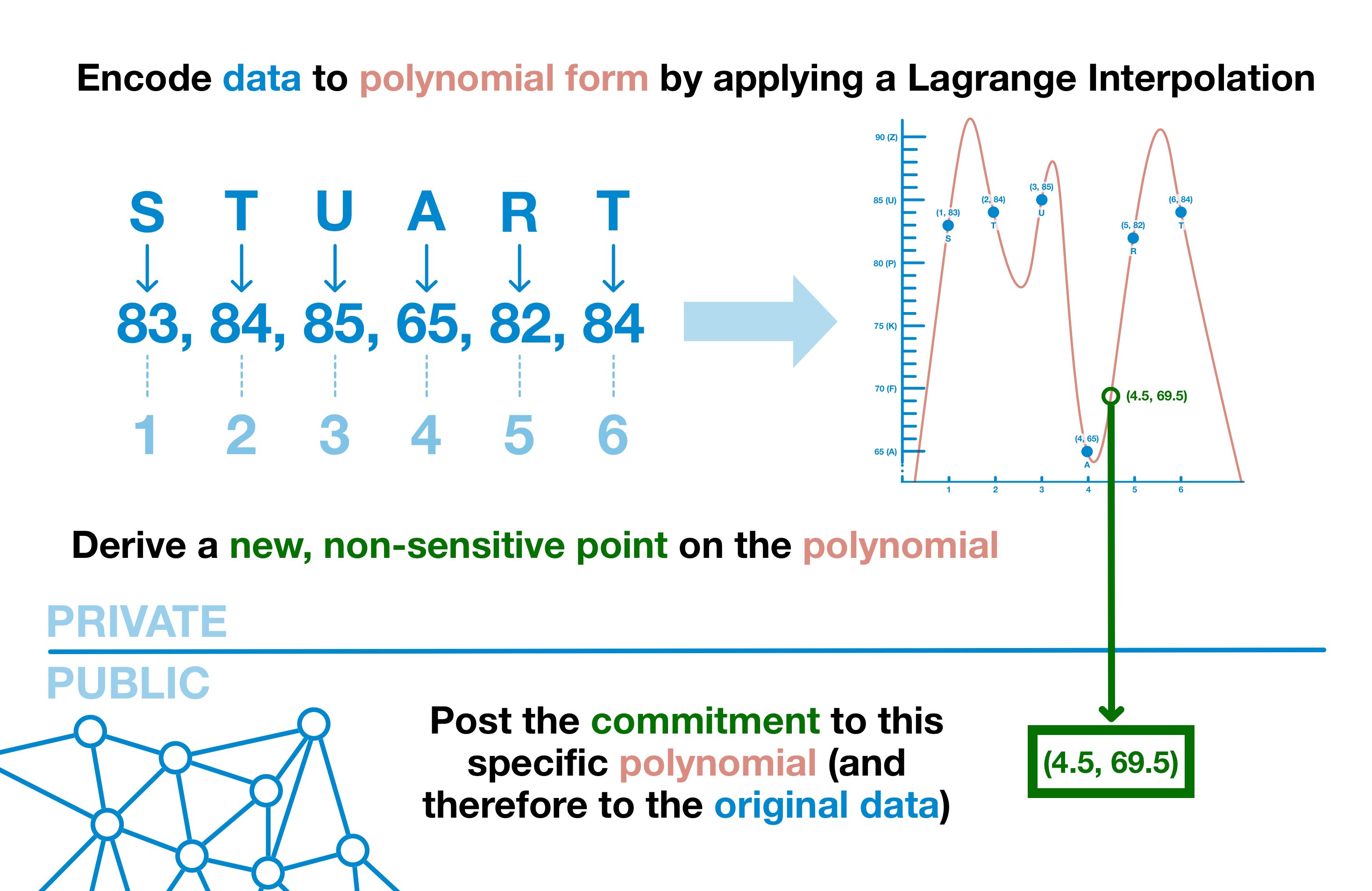
First and foremost, this point provides assurances that the data has not changed.
Just like a hash function, even a tiny change to the underlying data will have massive consequences for the resulting polynomial.
New data = new polynomial = new line. If the data changes so will the line, and the non-sensitive point we provided will no longer be valid.
As long as the point we post remains on the polynomial line, the public can be confident that we are working with the same data.
We call this non-sensitive point a "polynomial commitment" as its mere existence serves as cryptographic-proof that the creator is committed to working with the same polynomial.
A polynomial commitment acts a unique fingerprint for a specific set of data.
¶ Resources
Source Material - Twitter Link
Source Material - PDF