This is part 1 of a 3 part series on KZG Commitments. Here are links to part 2, part 3 and the summary article.

KZG Commitments Part 1: Commit

Prerequisites

Elliptic Curve Cryptography

Elliptic curve cryptography looks unapproachable, but it's totally understandable with a decent amount of high school algebra.

Check out this Into to Elliptic Curve Cryptography and you'll have the math you need to get through this article.

Pick a Number

Let's start with an example of a commitment scheme.

Example: Alice bets Bob he can't guess the number she is thinking of.

But Alice can change her number after Bob makes his guess, and so Bob isn't likely to take the bet. Instead, Alice writes down the number, committing to it.

After Bob's guess, she can reveal it.

A Hash-Based Scheme

There are many ways to commit to a specific piece of data, the key is to commit in a way that only obscures the data (instead of destroying it).

The most basic example of a commitment scheme is one based on a hash function.

Think of a hash function like a black box that takes some input data and irrevocably transforms it into a unique string of nonsense.

Imagine if Alice picks her number, hashes it and provides it to Bob.

By receiving the hash Bob wont have any new info to help him guess.

Once he gets Alice's answer (after guessing) he can hash it and check it against the original hash Alice provided.

The hash commits Alice to the underlying number, but does not leak any information.

The Problem with Hashing

The problem with hashing is that it is a very blunt and destructive tool.

Hashing creates a unique, non-reversible fingerprint - the same property that makes it a good commitment candidate also limits how useful it can be.

For example, let's say Carol has a list of 500 numbers and she wants to see if Dennis knows even one of them.

If Carol hashes the whole list, all 500 values get collapsed into a single hash. You can't tell if just one value is in that hash; it's all or nothing.

This is the problem space: how can we commit to a chunk of data in a way that allows us to check specific data points without revealing any extra data?

If I ask "if x = 1, does y = 4?"

We want to answer YES or NO; we do not want to leak any other information.

Polynomial Commitment Schemes

Deep Dive: Polynomial Commitment Schemes

Fortunately, we already know our solution: polynomial commitments!

Quick refresher: any data can be represented in polynomial form through a well-understood process called a Lagrange interpolation.

Data is discrete - it has a finite size with specific values.

To form the polynomial, we break the data into chunks, taking each chunk in order (x) and plotting our data (y).

Polynomial form allows us to derive y-values for ANY x-value, even if it doesn't really exist.

If our data is the word "STUART," we plot the following points:

[1, S]
[2, T]
[3, U]
[4, A]
[5, R]
[6, T]

Polynomial from allows us to calculate a value for x = 4.5, even though the result is a non-real, nonsense answer.

This is going to form the basis of our commitment scheme. We are going to commit to data by:

converting it to polynomial form
evaluating the polynomial at some non-sensitive point
sharing the evaluated value (referred to as the commitment)

Picking a Number

Here's the important question: which non-sensitive point are we going to use for our commitment?

If the inputs (x) we use to generate our commitment are publicly known, we run into a lot of issues. Most importantly, attackers can easily break and/or overcome the system.

A random number would be perfect; one that neither party knows beforehand (and therefore can't craft attack, producing correct values from the wrong underlying data).

But this is the internet, how are we going to get a random number like that?

Losing a Number Forever

Deep Dive: PCS Trusted Setup

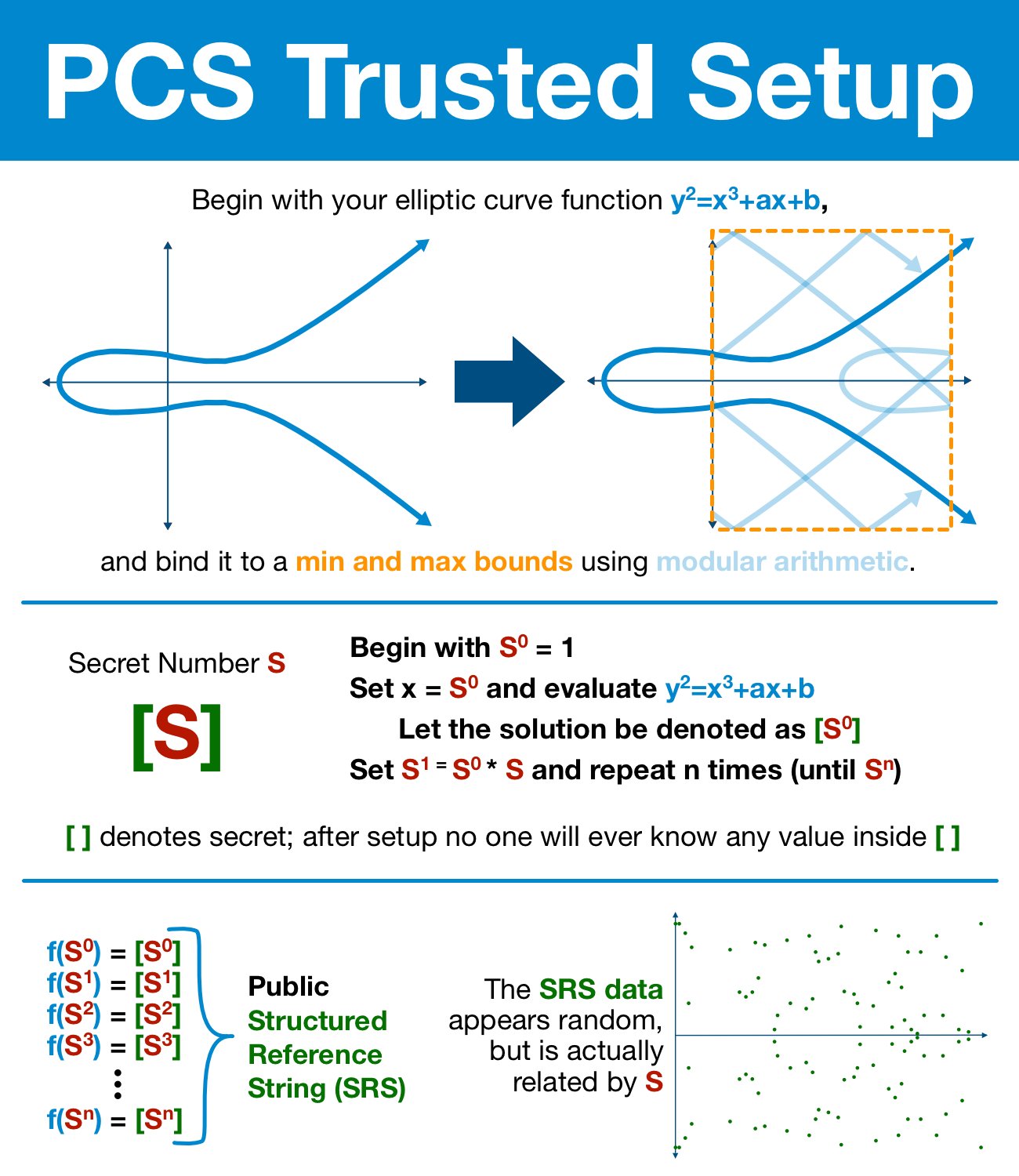
Once again, we've got our solution: an elliptic curve trusted setup! By the end of the setup, we will have irrevocably hidden a secret number (lost forever) in an elliptic curve.

And though the number is forever hidden, it's hidden in a particularly useful way.

Our setup provides us a list of numbers where each number is:

the secret number S
multiplied by itself i times
run through our elliptic curve function

Si is the fundamental building block of the SRS... the exact kind of term we need for our polynomial.

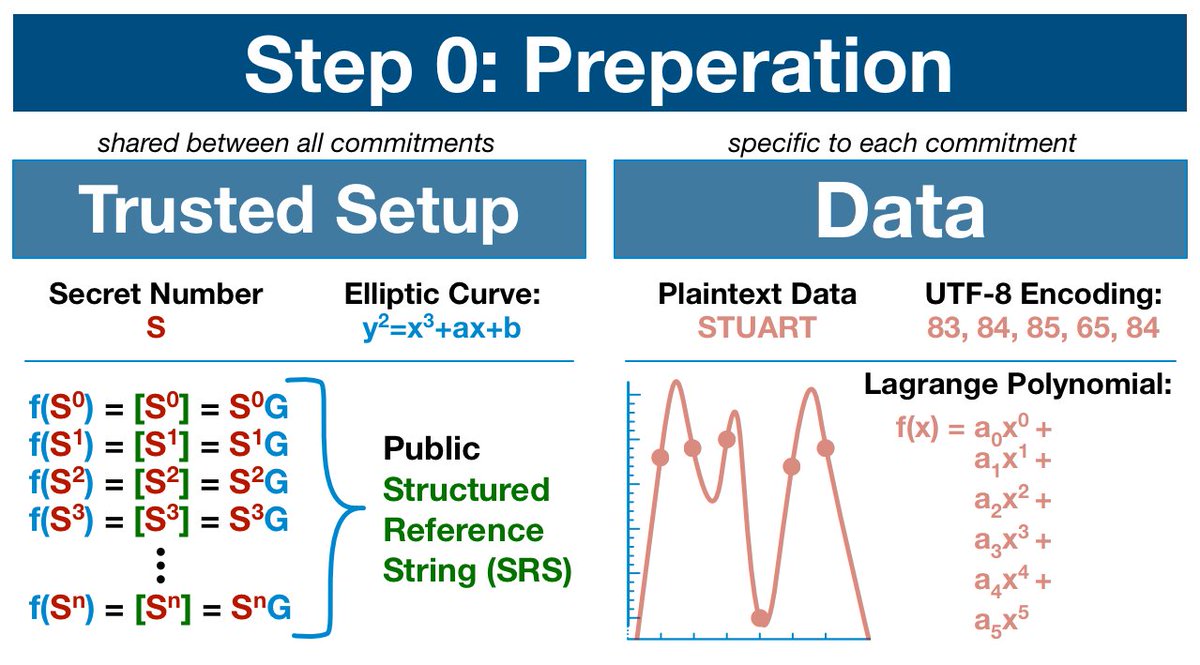
Notice how the terms created by the trusted setup (specifically the ascending exponent) resemble requirements of the data's polynomial (again, the ascending exponent).

Committing to an Elliptic Curve

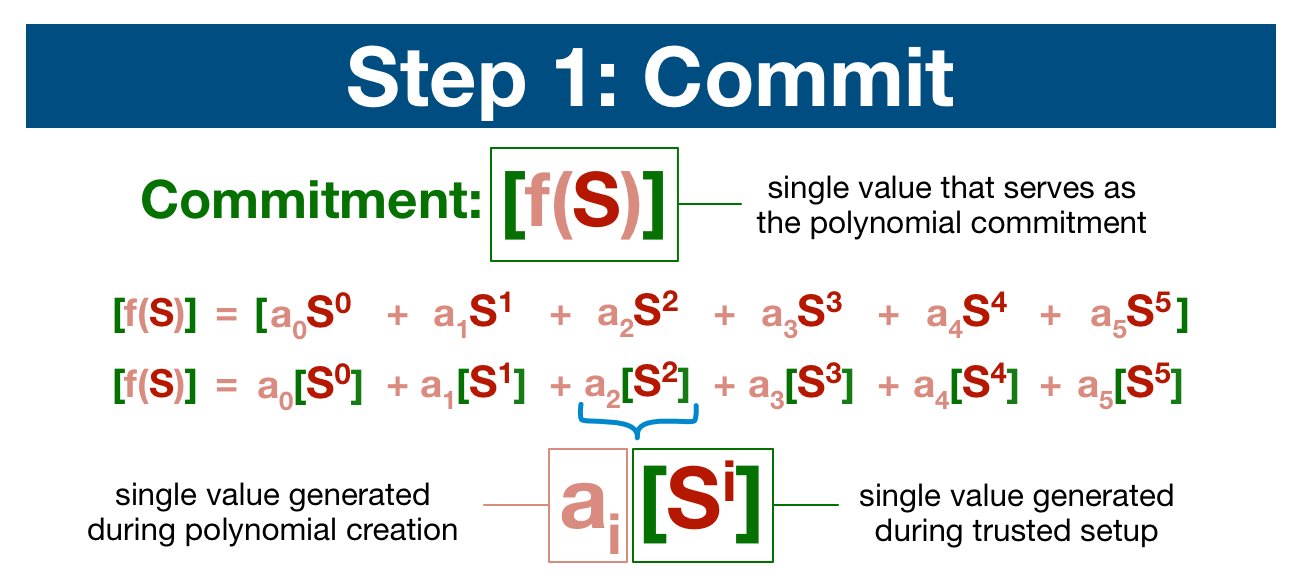
Now we are ready, we can commit to our data. We simply check how many terms our polynomial has, grab an equivalent number of points from the SRS and process the polynomial.

The result: you've been able to compute the value of f(S), even though S is permanently a secret!

In fact, our commitment is actually just another point on our elliptic curve! I've written out the (aggressively simplified) math below, but you don't need to worry about it.

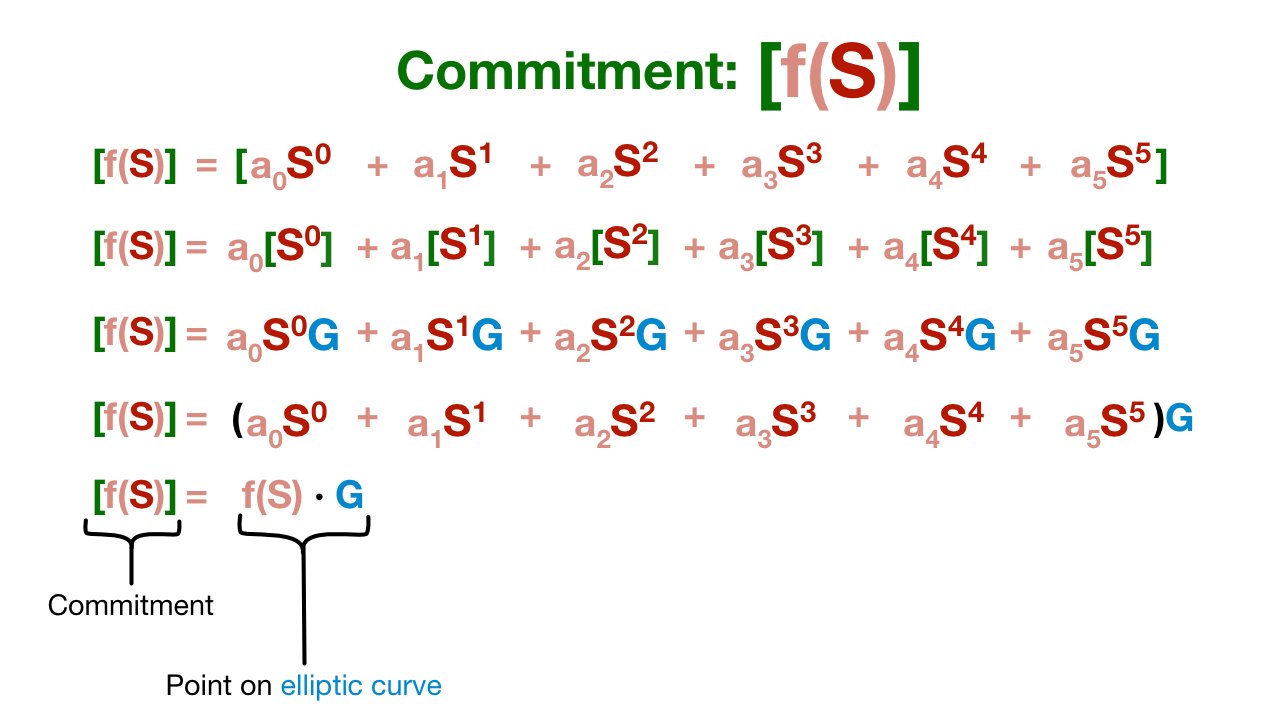
The important takeaway is simple: a KZG commitment is a point on the underlying elliptic curve.

Publicly Secure

Remember, our cryptographic scheme is built around the elliptic curve discrete logarithm problem: in an elliptic curve system, it is EXTRAORDINARY difficult to find X with only Xi.

And so our commitment can be publicly shared - any information stays secure.

And there we have our KZG commitment! Using the magic of elliptical curve cryptography, we are able to evaluate a function using a secret number.

One that no adversary could know before hand, because NO ONE knows it before hand.

Resources

Source Material - Twitter Link