This is part 2 of a 3 part series on KZG Commitments. Here are links to part 1, part 3 and the summary article.

KZG Commitments Part 2: Open

Prerequisites

Elliptic Curve Cryptography

Elliptic curve cryptography looks unapproachable, but it's totally understandable with a decent amount of high school algebra. 

Check out this Into to Elliptic Curve Cryptography and you'll have the math you need to get through this article.

Notation

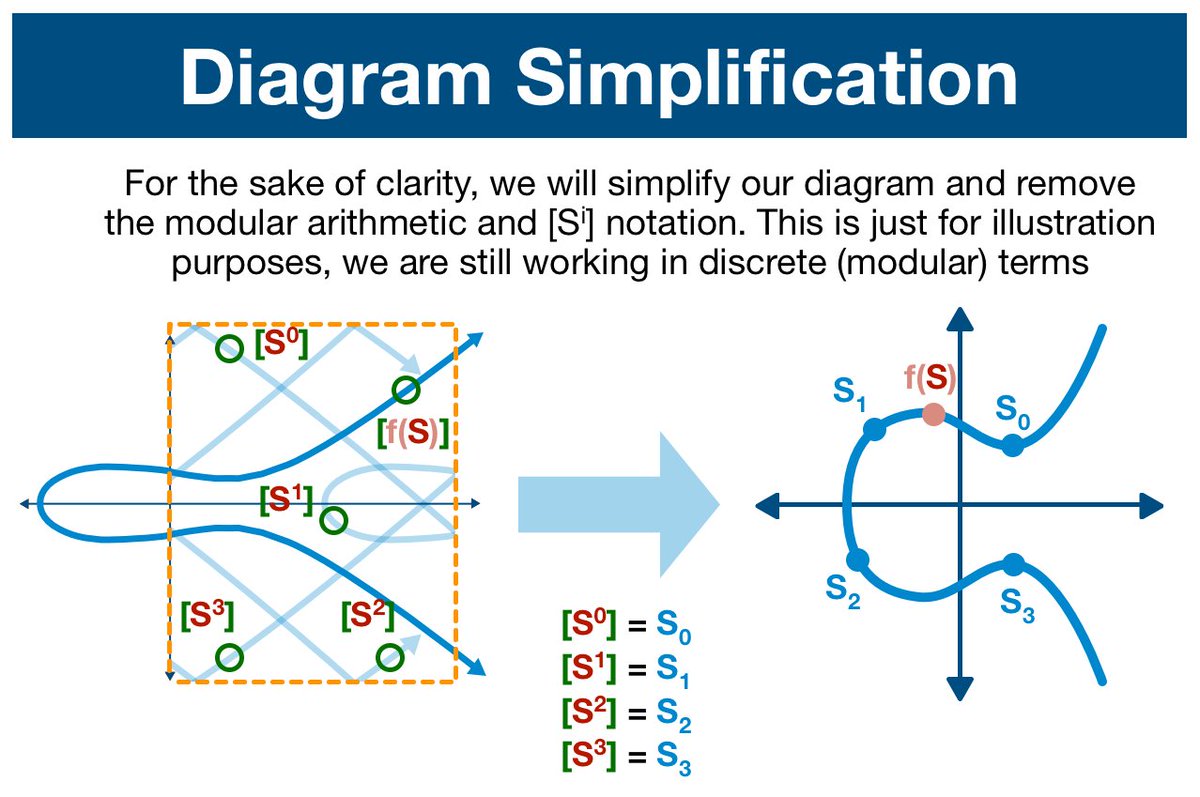
At this point our graphic has become too cluttered to be useful, so we will simplify in the name of readability. 

Nothing has changed, we are still working in modular arithmetic. 

KZG Commitment Scheme

Deep Dive: Polynomial Commitment Schemes

A polynomial commitment scheme allows one party to publicly commit to a specific dataset without giving away any info about the underlying data. 

Once a commitment has been calculated, the data is locked in; any changes to the data will result in invalid proof generation.

A KZG polynomial commit can be "opened" with any data point without revealing the entire dataset. 

Let's say I am thinking of 10 words. I write them each down on different pieces of paper. If you guess correct, i ONLY show you the correct 1 (keeping the other 9 hidden).

KZG Commitments Part 1: Commit

Deep Dive: KZG Commitments Part 1 - Commit

First, we generate a polynomial from our data using a mathematical process called a Lagrange Interpolation. 

Then, we calculate the value of this polynomial evaluated with a secret number S (hidden within an elliptic curve).

Once the commitment is calculated, the prover is bound to this specific data. The scheme is going to pivot around this specific value, derived from this specific polynomial. 

A change to even a single bit will result in a brand new polynomial (and therefore commit value).

Opening a Commitment

Now that the prover has been bound to this specific set of data, we can test the commitment by opening a proof at singular piece of data. 

The verifier, an independent entity who may or may not have access to the entire dataset, now chooses a piece of data to verify.

Let z be the piece of data the verifier is going to test... and so he sends z over to the prover. 

First, the prover calculates f(z). 

This is very easy for the prover; he has already built the polynomial in order to generate the commitment. He simply runs z through.

Dividing Polynomials

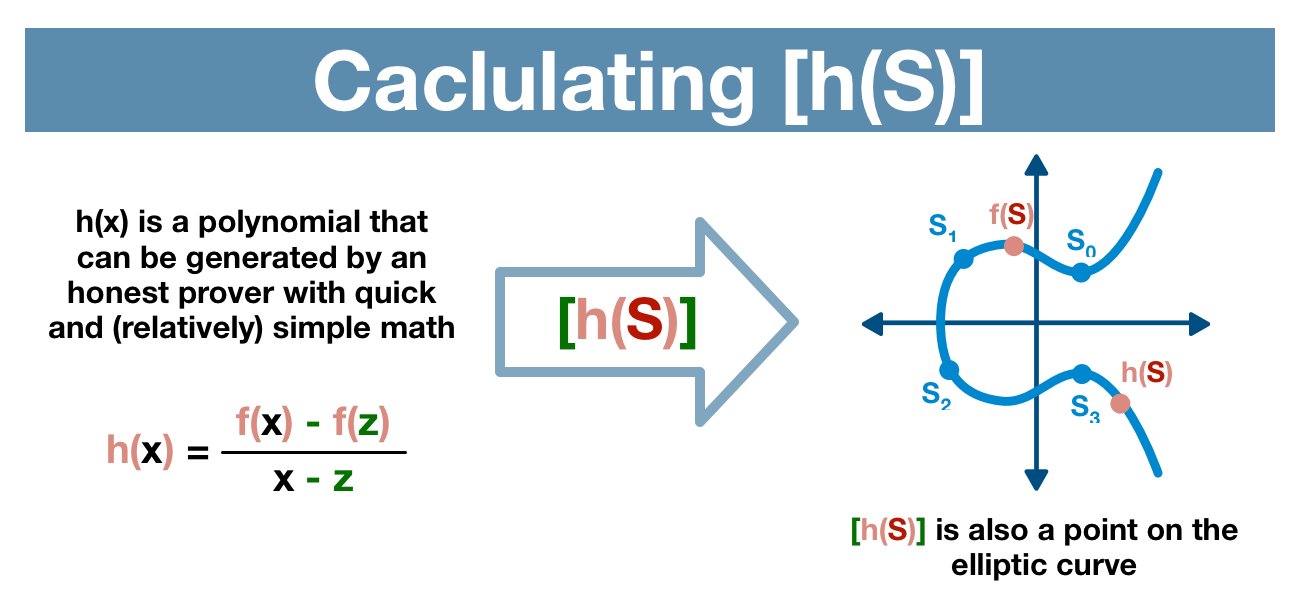
We are going to hand wave through the math, but here's a great resource to learn more.

tl;dr you can divide polynomials. It's not a particularly complicated operation, in fact it (can) look like long division. 

Because the prover has built the polynomial, it is very easy for them to create the new polynomial h(x). 

h(x) is the quotient polynomial built off of our proof data z.

Summary

The important takeaway: the verifier provides a value (a piece of data in the dataset to which the prover is committed) around which the prover is going to create an elliptic curve point and one other value.

And that's it! Our commitment is open and the prover has created all the pieces that the verifier needs to verify the proof! 

Resources

Source Material - Twitter Link