¶ KZG Commitments
¶ Prerequisites
¶ Elliptic Curve Cryptography
Elliptic curve cryptography looks unapproachable, but it's totally understandable with a decent amount of high school algebra.
Check out this Into to Elliptic Curve Cryptography and you'll have the math you need to get through this article.
¶ Interactive Proof System
Interactive Proof System: a method by which one party (prover) can prove to another (verifier) that a statement is true.
¶ Polynomial Commitment Schemes

Deep Dive: Polynomial Commitment Schemes
Before we get to KZG, let's first cover the basics: polynomial commitments.
First, take your dataset and break it into discrete chunks.
Then, plot them on a graph and draw a line through those point.
Now derive the formula for that line.
This formula is a polynomial, a special type of equation that has some very powerful mathematical properties. This polynomial holds the same information as the raw data, but we can also use it to generate new points... maybe a point in between two "real" points.
In fact, one of these "non-real" points will serve as our commitment: it confirms a party has complete knowledge of the dataset (else they would not be able to generate the polynomial) but it does not leak any of the underlying data.
Now, which "non-real" point to use...
¶ PCS Trusted Setup
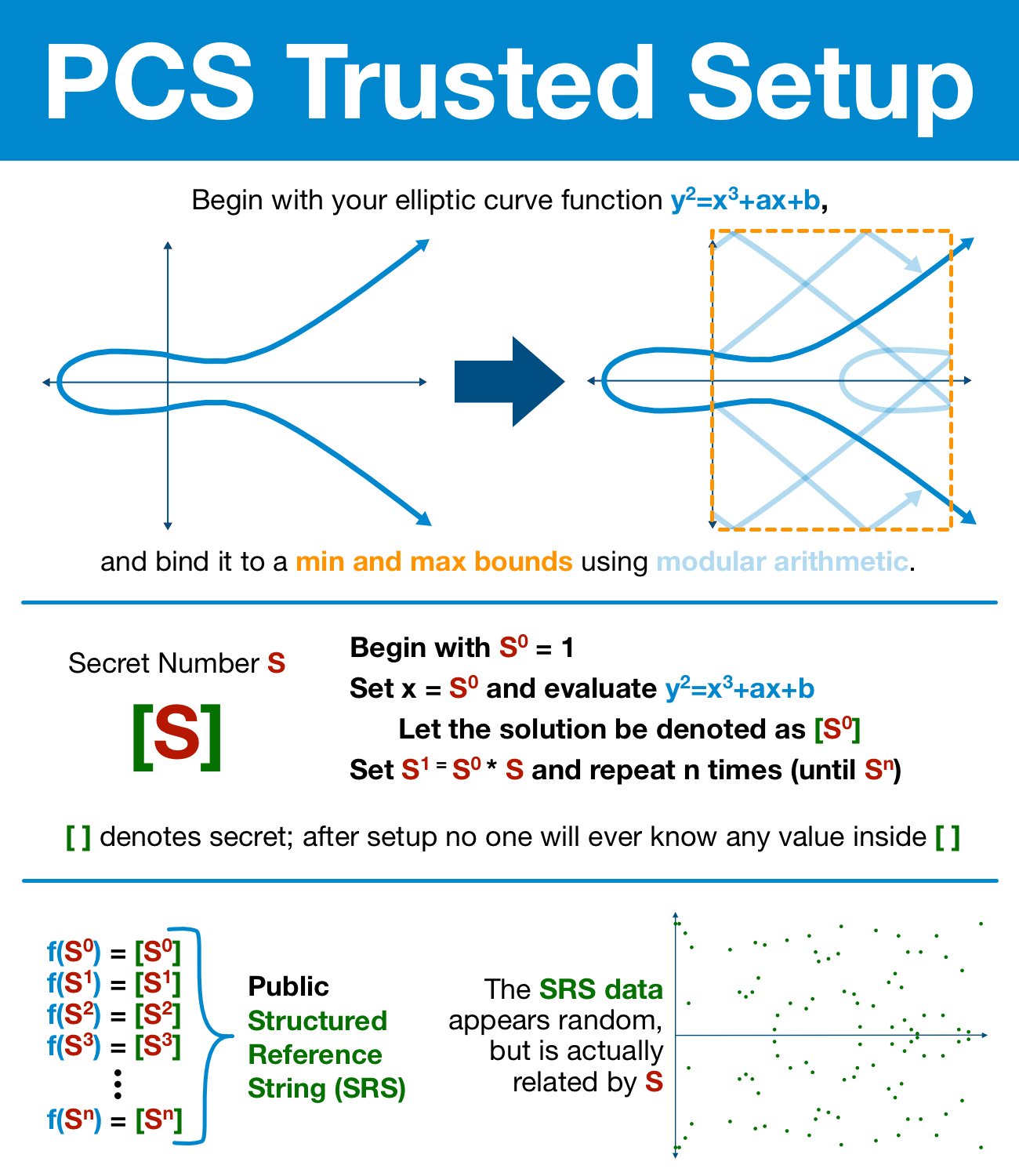
Ideally we'd like to use a completely random point, one that no malicious party could know beforehand. Then the prover couldn't precompute some points that look valid, but don't actually check out.
Finding the random number isn't particularly difficult, it's keeping it secret that's a problem. We're going to have to use an elliptic curve!
(Modular) elliptic curves have many incredibly useful properties that we will be relying on. In particular, we care that:
- elliptic curve points can be added together
- when added repeatedly, it is INCREDIBLY difficult to figure how many times a point has been added
Using these properties, we can hide a secret (random) number inside an elliptic curve.
After we go through the trusted process and the secret number is permanently destroyed, the only knowledge of that value will be permanently hidden in the folds of the elliptic curve.
The result of the trusted setup is a Structured Reference String (SRS). The SRS conveys enough information that the random number is accessible for our polynomial (and therefore our polynomial commitment scheme) while still keeping the value entirely secret.
Note: one SRS can be used by an arbitrary number of people; only one trusted setup (or one trusted setup per application) are needed for ALL KZG commitments.
¶ KZG Commitments
Kate-Zaverucha-Goldberg Commitments, also called Kate Commitments, polynomial commitment scheme.
Once we have our SRS and we've generated the polynomial from our data, we are ready to begin.
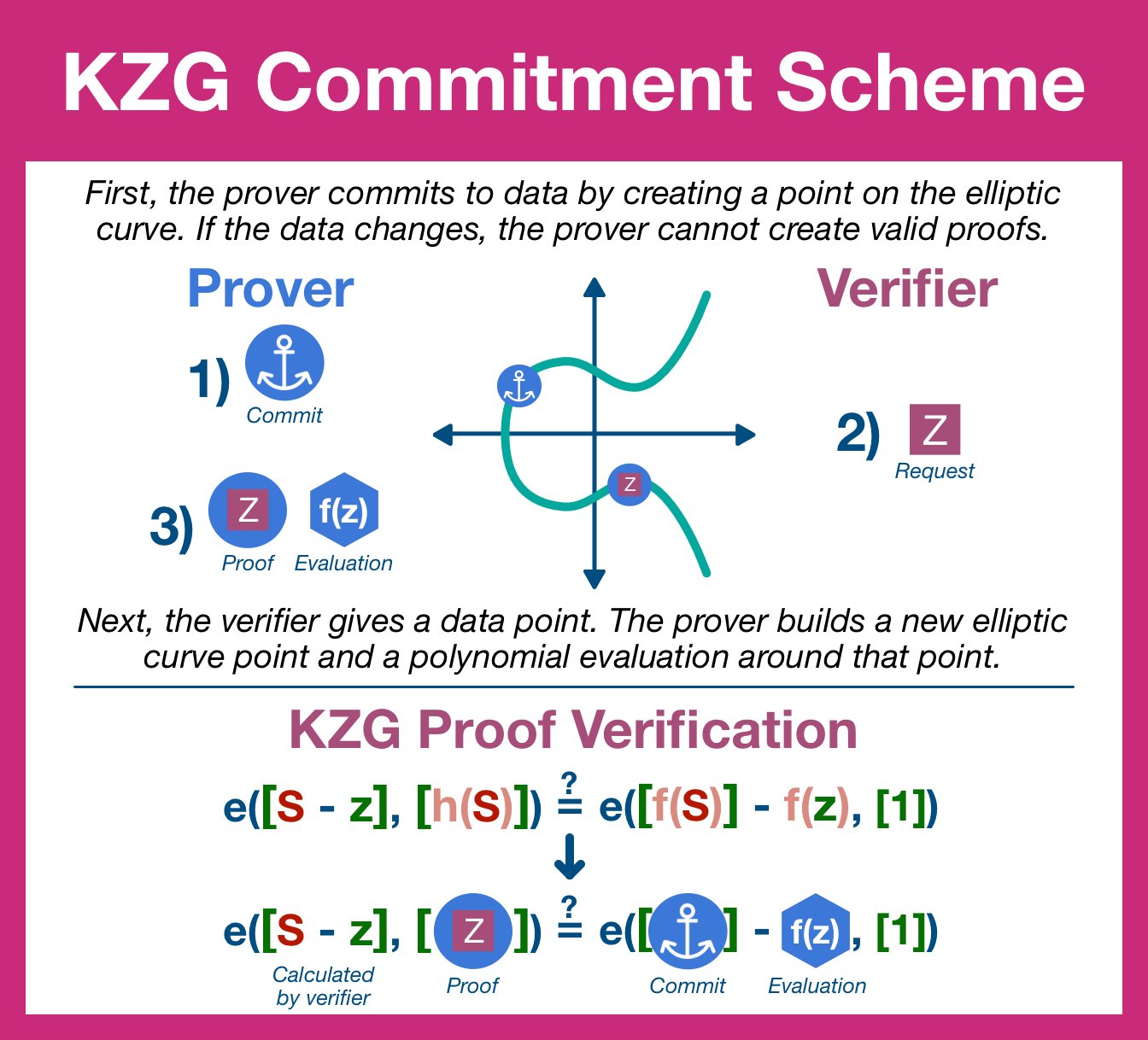
¶ Step 1: Commit
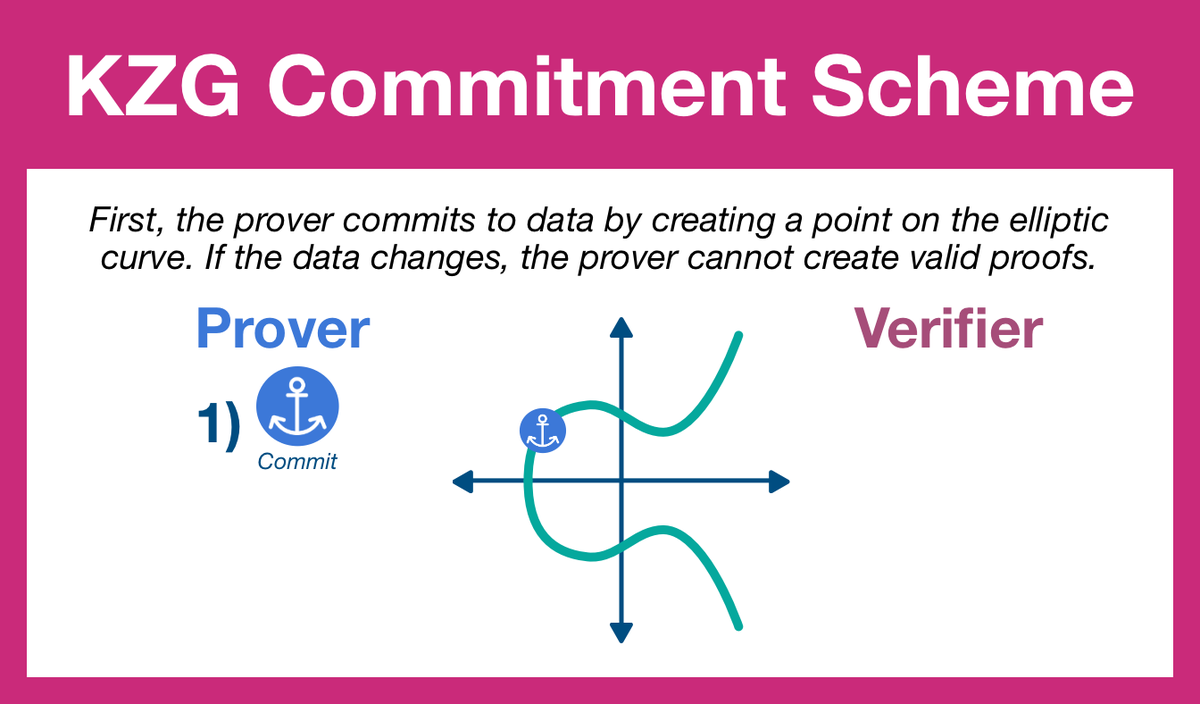
The prover is going to begin by applying the SRS to the data polynomial, generating a point on the elliptic curve.
We call this point a commitment.
The commitment will serve as an anchor, tying the prover to the original dataset. Any changes to the underlying data will result in a new polynomial and therefore a new commitment.
Changes to the data = previous commitments will generate invalid proofs.
¶ Step 2: Open
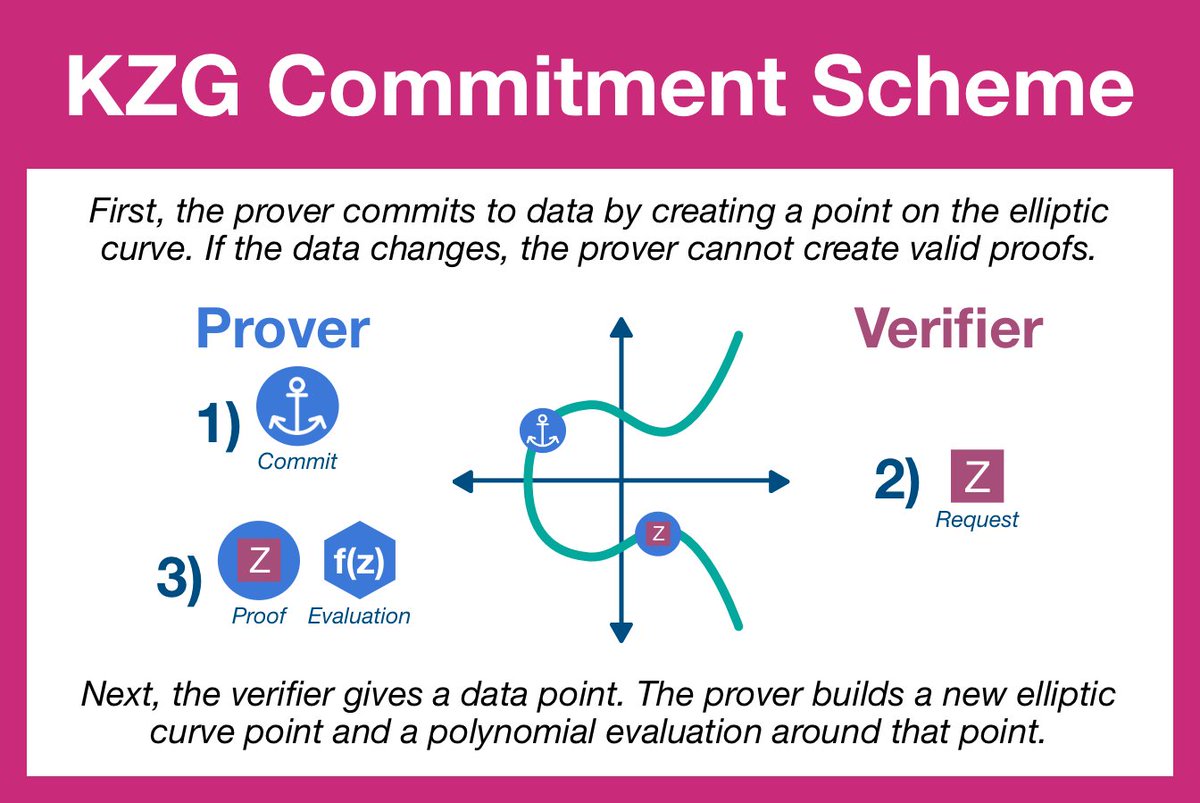
Now it's time for the verifier to test the prover.
The verifier will select a position and request a proof based around that specific chunk of data. The prover will divide the data polynomial to create a new quotient polynomial.
This division is the crux of the KZG commitment scheme. Polynomial division is a (relatively) easy procedure; as long as an honest prover has full access to the data (and therefore the data polynomial), he can create and evaluate this new quotient polynomial.
¶ Step 3: Verify
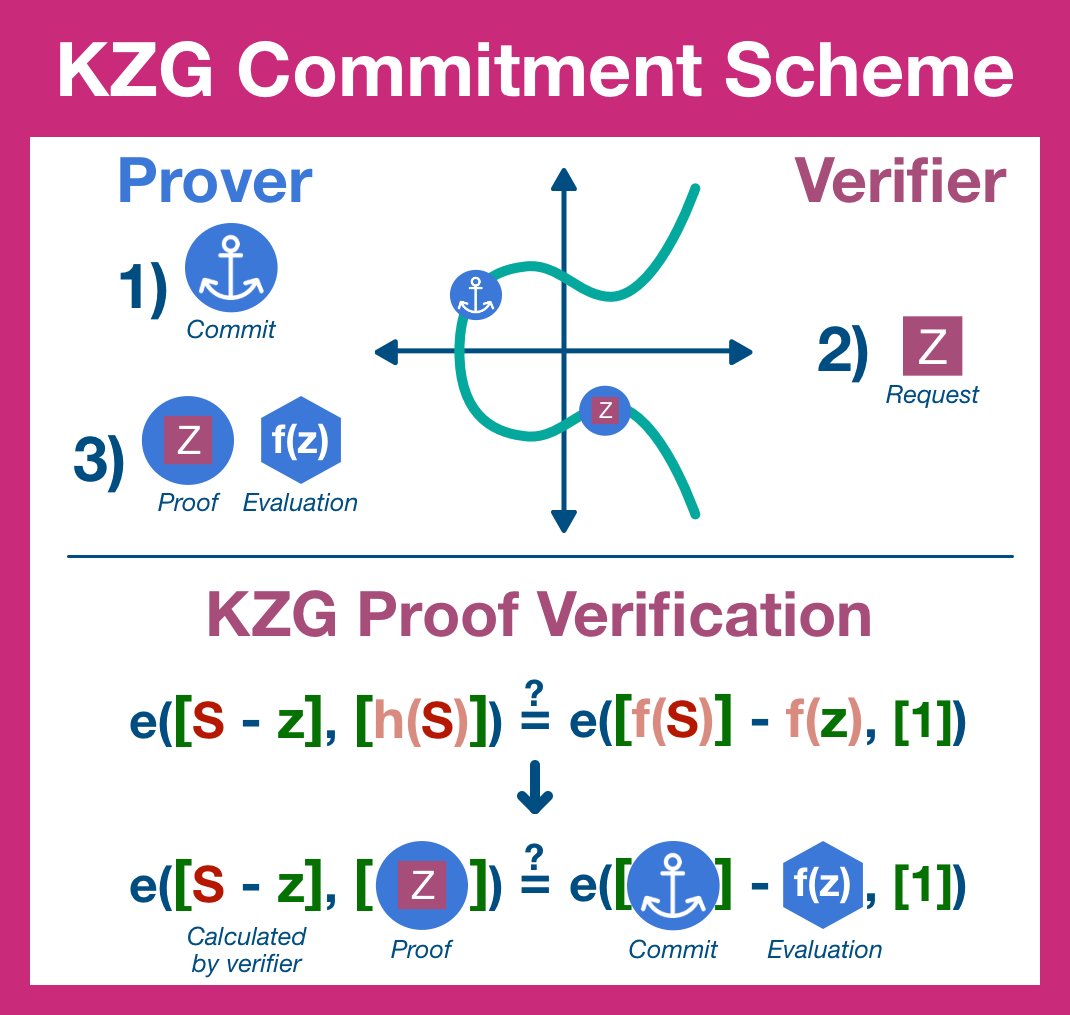
The prover replies back with two items: the evaluation of quotient polynomial using the elliptic curve and the result of the polynomial evaluated at that position. The former is an elliptic curve point, the later the data polynomial evaluation.
Before we move on, let's consider the polynomial evaluation. Remember, the polynomial is an expression that describes how our data looks when plotted on a graph. The evaluation of that function is simply just the data at that position!
To finish our proof cycle, the verifier (who does not have access to the full dataset and therefore cannot generate the data or quotient polynomial) is going to ensure the provers response reconciles with the commitment.
But first, we are going to need one more tool.
¶ Elliptic Curve Pairings
Deep Dive: Elliptic Curve Pairings
In order to combine the pieces sent by the prover, the verifier is going to need to multiply elliptic curve points.
Unfortunately, this just isn't possible; that's not how elliptic curves work.
Fortunately, we have a substitute: elliptic curve pairings.
And now, finally, we are ready to verify our proof.
The verifier constructs two expressions and checks them for equivalence. If they are equivalent, the verifier can be certain that the prover did the (polynomial) division and therefore still has the original data.
¶ Summary
The commitment acts as an anchor, a proof entails quick polynomial division and verification is a simple check.
The verifier can know with mathematical certainty that the prover is honoring their commitment; whatever data is there is the same that created the commitment.
So, in summary, a KZG commitment is a polynomial commitment scheme used to bind a prover to a specific set of data.
KZG commitments also have a very useful feature: they can be opened (audited) at any position without revealing any unrelated data.
¶ Resources
Further Reading:
- KZG polynomial commitments - Dankrad
- Kate Commitments: A Primer - Walpo
- KZG Commitment Workshop - Dankrad
- Introduction to Elliptic Curve Pairings - Dan Boneh
- What is PLONK?
- Exploring Elliptic Curve Pairings - Vitalik
- How do trusted setups work? - Vitalik
- Factoring - Ben Lynn
- Original KZG Paper
Source Material - Twitter Link
Source Material - PDF