
Commitment Schemes
Public Assurance
Let's say you have a large amount of data that, for whatever reason, is private. How can you provide a public audience assurance that you will not alter the data without allowing them to see it?
The naive approach breaks our problem statement's basic privacy assumptions. Revealing the data allows public verification... at the cost of 100% of privacy.
We need to find a way to provide a unique fingerprint of that specific set of data to act as a signature.
Commitment Schemes
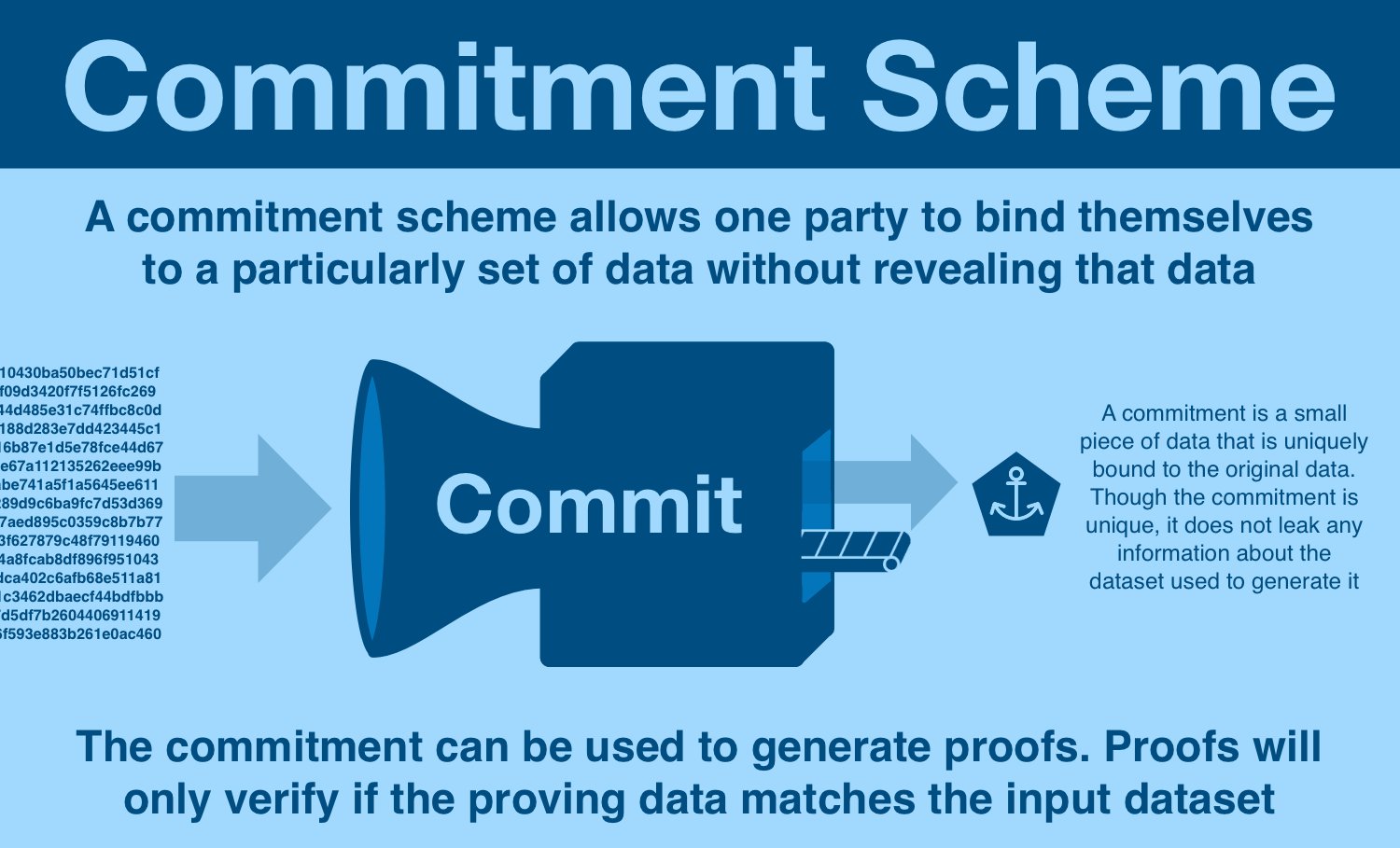
Here's the rough schematic of commitment generation:
- start with data of arbitrary contents and size
- feed data into a commitment scheme
- commitment scheme generates a commitment, unique to a specific dataset
The commitment is some unique piece of data that inseparably bound to the original dataset. Each dataset will generate a different commitment, and each commitment corresponds to a different dataset.
The trick: it is (almost) impossible to go from commitment → dataset.
Because it is INCREDIBLY difficult to go from commitment to dataset, it can be publicly shared without any fear of leaking any of the underlying data.
If we stopped here, we'd still have something useful; digital fingerprints are just as useful as the IRL version.
But we aren't going to stop here, a commitment scheme has a second act: the commitment can be opened!
We still cannot go from commitment to dataset; instead we can combine the commitment with a proof to verify the underlying data.

Examples
Too abstract; let's run through some examples:
- Alice is a patron of both BigBank and InsureCo and is processing a transaction that requires both. Instead of communicating it in public, BigBank and InsureCo commit to the same data and share commitments.
- Government worker Bob is distributing [thing] to eligible citizens, but can only identify people through sensitive information (eg a social security/national ID number). Bob shares a commitment to the dataset, which people can use to verify their eligibility.
- Charlie is building blocks for mev-boost. At auction, he cant reveal the block, else someone will just copy it and undercut him. Instead, he submits a commitment, binding him to a block that can be revealed if and only if it is chosen.
In summary, the purpose of cryptographic commitment schemes is to publicly bind one party to a specific set of private data in a way that can be revealed later.
Implementation
But not all commitment implementations are equal; some are more capable than others. 3 examples...
Hashing
- Commit: hash your dataset to generate a random-looking string
- Open: reveal the data, making it available for others to hash
- Verify: check the self-computed hash against the commitment
While this scheme checks all the boxes of being a commitment scheme, it isn't particularly useful. Opening is an all-or-nothing prospect.
Not only does this have (obvious) implications for privacy, it has pretty aggressive bandwidth assumptions.
Merkle Trees
- Commit: generate the tree by applying rounds of hashing between nodes until a single root is remaining
- Open: provide a piece of data and the required inner nodes to self-compute the root
- Verify: compare the self-computed root to the commitment
In comparison to a simple hash-based scheme, Merkle trees are an enormous improvement.
First, the commitment can be opened privately at an individual point. The opener will need the inner nodes, but those can be shared without leaking any data in the underlying dataset.
Second, the Merkle trees are MUCH more efficient than a hash-based scheme. Instead of transmitting the entire dataset, Merkle proofs require O(log n).
For those of you with a life, O(log n) just means the proof size grows exponentially slower than the dataset size.
Quick aside, while Merkle trees are a huge improvement, they are not perfect. This O(log n) idea is a double-edged sword. Yes, it does grow slower than the dataset, but it will grow, relentless and unceasingly.
KZG Polynomial Commitments
Tl;dr KZG commitments allow a party to commit to a dataset in a way that can be opened at any point.
However, unlike Merkle trees, KZG commitments have a constant proof size.
You can prove any amount of evaluations (think millions) with just one 48 byte piece of data!
Summary
By now, you've definitely got it. A commitment scheme is about creating commitment that is anchored to a piece of data.
Schemes that can be opened at specific points are particularly useful; the questions are just of commitment calculation efficiency and proof size.
Resources
Source Material - Twitter Link