¶ Ethereum State Expiry
¶ Prerequisites
¶ Ethereum State Machine
A state machine is a mathematical model of computation with two major components:
- the state, the configuration of the system at a moment in time
- a transaction, the set of instructions to change the state
The state transition machine model provides a simple framework for breaking down computation into a step-by-step process.
¶ Merkle Trees, Merkle Proofs and Merkle Proof Scaling
A Merkle tree is a (tree) data structure in which each leaf node is labeled with the cryptographic hash of a data block, and each non-leaf node is labeled with the cryptographic hash of its child nodes' labels.
A Merkle proof can be used to efficiently prove that a single piece of data exists in a dataset without transferring the entire dataset.
Although a Merkle tree still is much more efficient that transferring the entire data set, the Merkle proofs are getting so large we are running up against the same barriers.
¶ State Size Management Theory
Vitalik's Theory of Ethereum State Size Management:
- Unbounded growth - state unrelentingly grows over time
- State expiry - unused state becomes inactive
- Weak statelessness - block producers need the full state
- Strong statelessness - no nodes need the full state
¶ The World Computer
Ethereum, the World Computer, exists between a network of 1,000s of computers (nodes), each running a local version of the Ethereum Virtual Machine (EVM).
The nodes provide the hardware, the EVM provides the virtual computer and the blockchain records Ethereum's history.
The EVM sits at the center of Ethereum, providing a decentralized computing platform to the world.
Everything is designed to construct this virtual machine and expose it to the world, so that anyone who is interested can permissionlessly interact with it.
The internal state of the EVM is stored in a data structure known as a Merkle tree.
Merkle trees are very powerful, but they are not perfect.
Specifically, they don't scale efficiently enough for the World Computer.
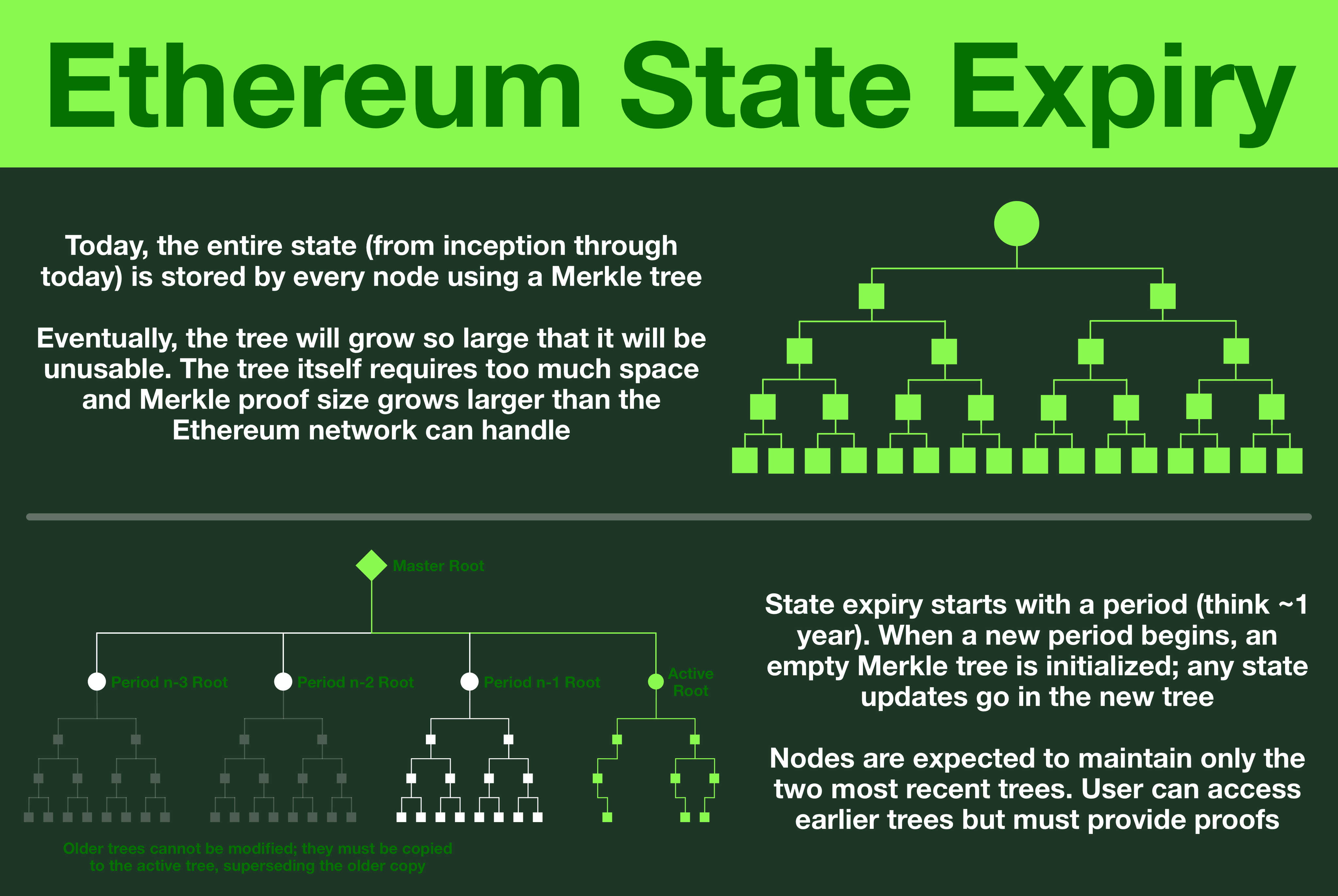
Today, the World Computer stores the entire state of the EVM; every account, every entry, all the way back to genesis. For now, that amount of data is acceptable, but without intervention the size of the state will grow to infinity.
We'll kiss decentralization goodbye.
¶ State Expiry
Fortunately, the gigabrains developing Ethereum have been thinking ahead for a while now. And so, we have a framework out of which to build potential solutions.
In particular, we are interested in the concept of state expiry.
With state expiry, parts of the state default to inactive and must be explicitly renewed.
While there are many ideas around renewal, we are particularly interested in schemes that refresh via "touching;" simply accessing the state is enough to defer expiry.
State expiry keeps the size of the EVM's state at a manageable level; nodes will be allowed to offload stale data in order to make room for new objects. Over time, the state size should remain (somewhat) stable, configurable by the scheme we decide to implement.
In any (good) state expiry scheme also has a method to revive expired/inactive parts of the EVM state.
Think of it this way: each node holds the last X days of state, if you want to access further back, you must provide proof it existed in the state >X days ago.
¶ A State Expiry Proposal
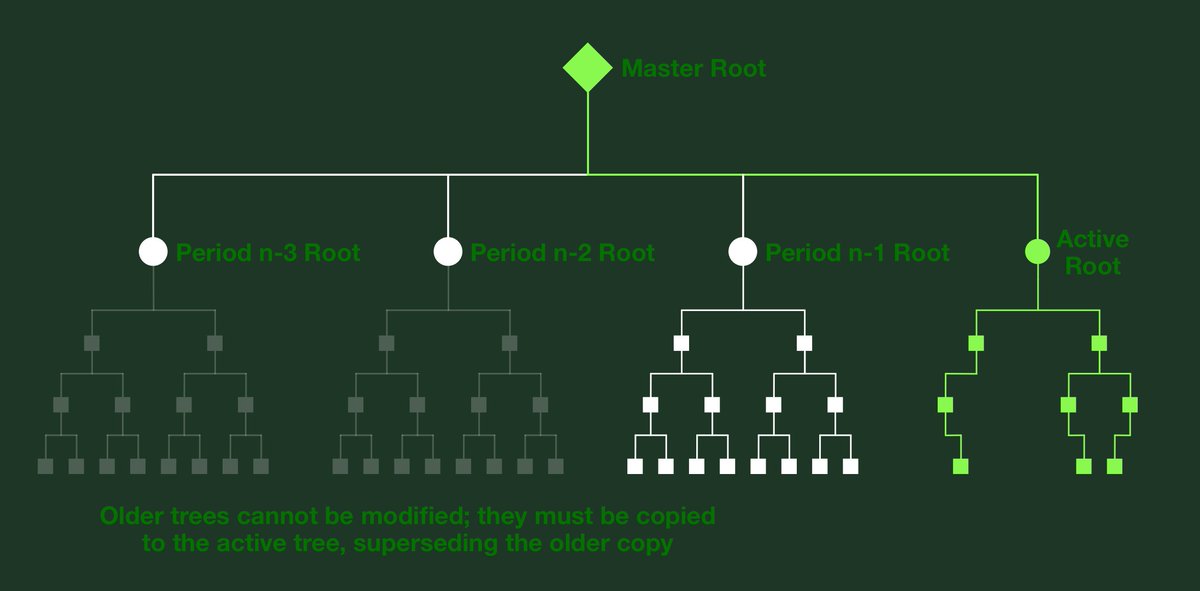
Here's the state expiry scheme we are interested in.
Each period (~1 year) Ethereum will archive the current state tree and will initialize a new state tree.
Archived trees cannot be modified; any changes to objects require first copying them over to the new state tree.
Each node is required to hold a certain number of archived trees (proposal: 1 archive tree plus active tree).
When a period ends, a node is free to release older trees.
Thus, the EVM state size remains manageable; at most it will be two full trees covering 1 period each.
¶ Recovering Expired Data
While nodes (can) release the older archive trees, they keep the Merkle root in perpetuity (this is a single string, does not introduce scaling issues).
Reviving a piece of the inactive state is as simple as providing the Merkle proof for that old state.
Ok in reality it's not quite so simple, but it's still straightforward. The section below basically says "if the state is active, modify it. If it's inactive, you have to prove that it was part of the state, is now inactive, and was not accessed between now and then."

¶ Revisiting Statelessness
Interestingly, this state expiry scheme reframes our conception of statelessness.
At the network level, this isn't stateless as nodes still need to hold the most recent state, but for objects older than "most recent," we can access the state solely via Merkle proofs.
Let's say we follow the proposal and allow nodes to release archive trees that are older than 1 period.
Well, some node operators might choose to store a few extra, just to optimize proof generation. And we could create state-archive-nodes which hold every tree.
We can also go in the opposite direction. Again, assume the proposal's rule of 1 archive tree. Theres no reason you MUST access the state through the tree; you could verify using only Merkle proofs.
Then the question becomes, why hold any of the trees at all?
What's interesting about state expiry schemes is that they offer a way for different nodes to access different levels of statelessness based on their specific needs.
Gas costs (and the like) will be optimized for 1 archive tree, but the choice is the node operator's.
¶ State Expiry and Ethereum
State expiry is a very exciting and important area of Ethereum research. Bottom line, we are going to need to implement some sort of scheme.
But thing's aren't quite so easy. Picking a scheme is one thing, implementing it is a whole other animal.
We are talking about changing the data structures that hold the state of the EVM, the molten core of Ethereum.
It cannot be overstated how delicate and high stakes a task this will be.
Fortunately, we have some experience with these kinds of things.
¶ Resources
Source Material - Twitter Link
Source Material - PDF