¶ Merkle Tree Scaling
¶ Prerequisites
¶ Hashing
Applying a hash function takes data (of arbitrary contents and size) and reduces it to a unique, compact string.
Every input produces a unique output, even if two inputs are nearly identical.
¶ Merkle Tree
A Merkle tree is a (tree) data structure in which each leaf node is labeled with the cryptographic hash of a data block, and each non-leaf node is labeled with the cryptographic hash of its child nodes' labels.
A Merkle proof can be used to efficiently prove that a single piece of data exists in a dataset without transferring the entire dataset.
¶ The World Computer
Ethereum exists between a network of 1,000s of computers (nodes), each running a local version of the Ethereum Virtual Machine (EVM). All copies of the EVM are kept perfectly in sync.
Any individual EVM is a window into the shared state of the World Computer.
¶ Merkle Trees
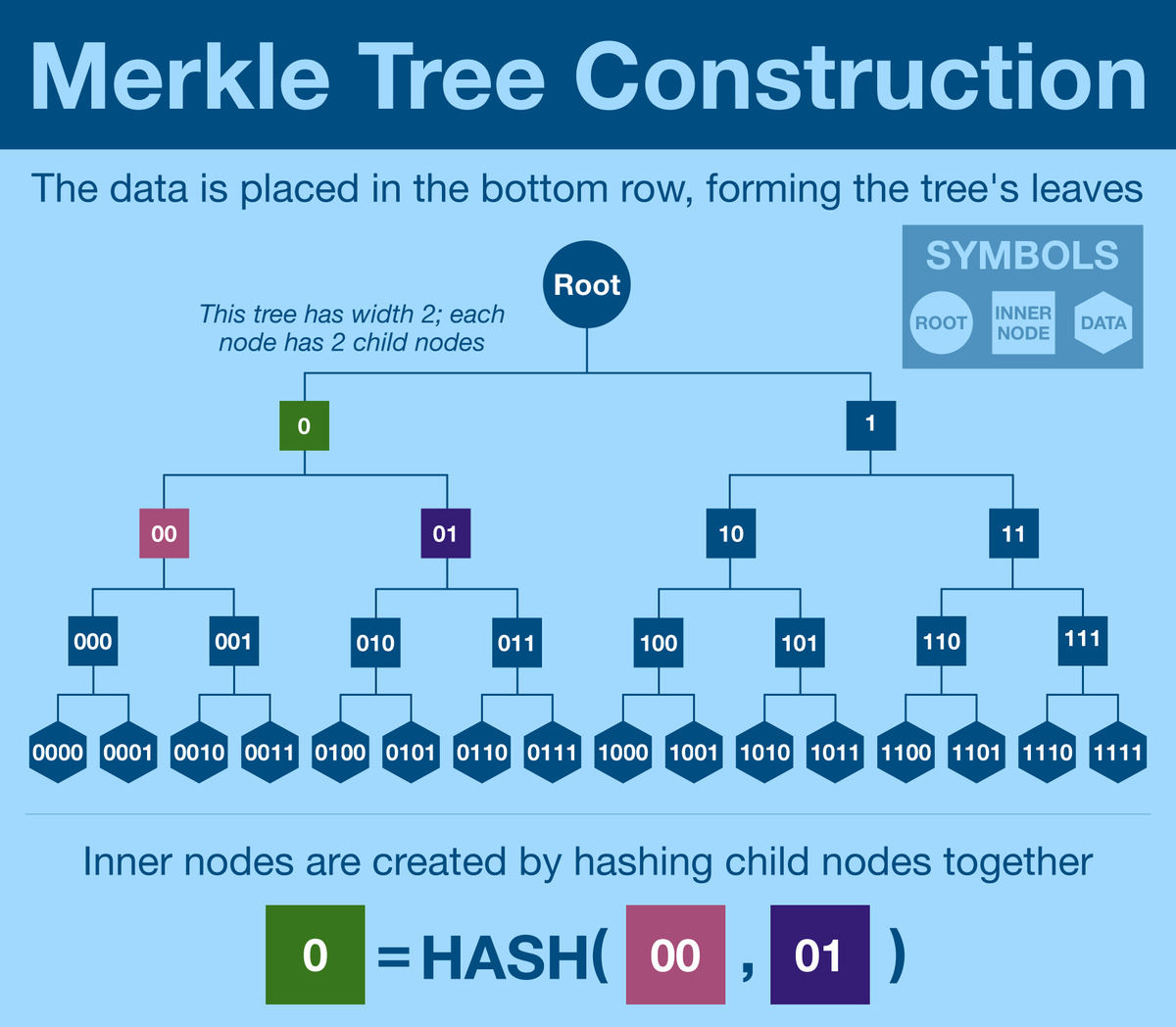
A Merkle Tree is a data structure that allows the efficient verification of the contents of a large dataset.
Merkle Trees are made by successive rounds of hashing (applying a hash function to a set of data). A hash function transforms data of arbitrary contents (and length) into a unique, compact string.
Think of a hash like a unique serial number for a set of data.
We begin by placing our data into the bottom row and picking a tree width (number of children per node). To move up a level, we simply select [width] number of nodes and hash them together. This continues until a single hash is reached.
We call this hash the Merkle root.
Remember, hashing creates an identifier for whatever was put into the hash function. This method will generate a unique string for each node, irrevocably tied to the underlying dataset.
Any changes to the data will require updating the tree, all the way up to the root.
Once we have our Merkle root, we are in business.
¶ Merkle Proofs
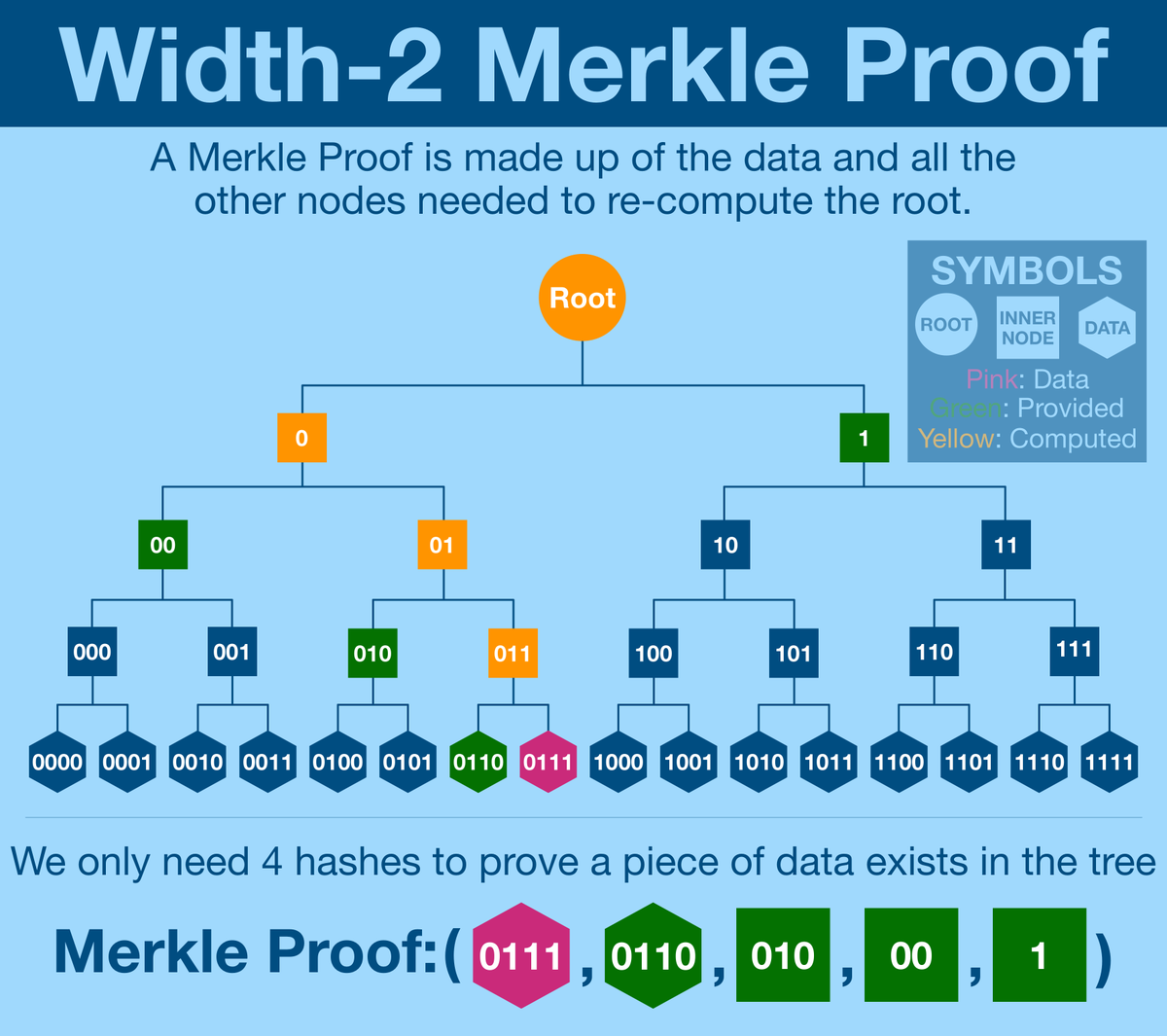
The root is a lightweight string that can be used to verify any single piece of data in the associated Merkle Tree. Your tree can have billions of items, yet our Merkle root can verify even a single datum spec.
We call the trick a Merkle proof; rather than transfer the entire dataset, a user can send a single data point AND the hashes that make up the intermediate nodes of the Merkle Tree. Using just the branches and the data point, a verifier can rebuild the Merkle root.
If we didn't use computer science, (basically) the only way to verify a piece of data is in the dataset is to pass the entire dataset.
The Merkle Tree is a huge improvement, drastically reducing the amount of data transmission needed to verify the point.
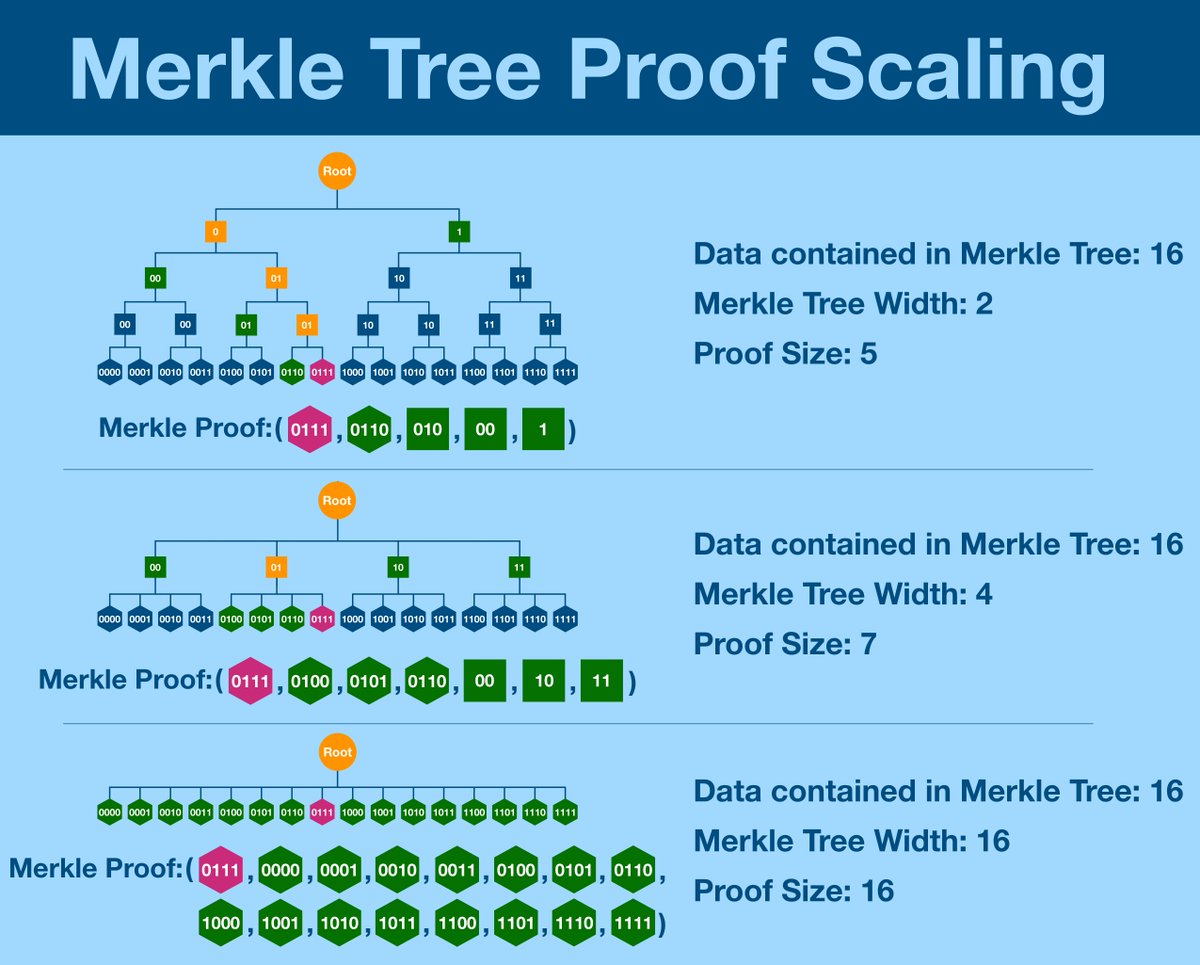
¶ The Optimal Merkle Tree
Now, you might look at the graphic above and notice something: most of the components of the Merkle proofs are inner nodes (squares).
What if we could reduce the number of inner nodes by increasing the width (and therefore decreasing the height) of the tree?
Let's take a look at a wider tree, one with width 4.
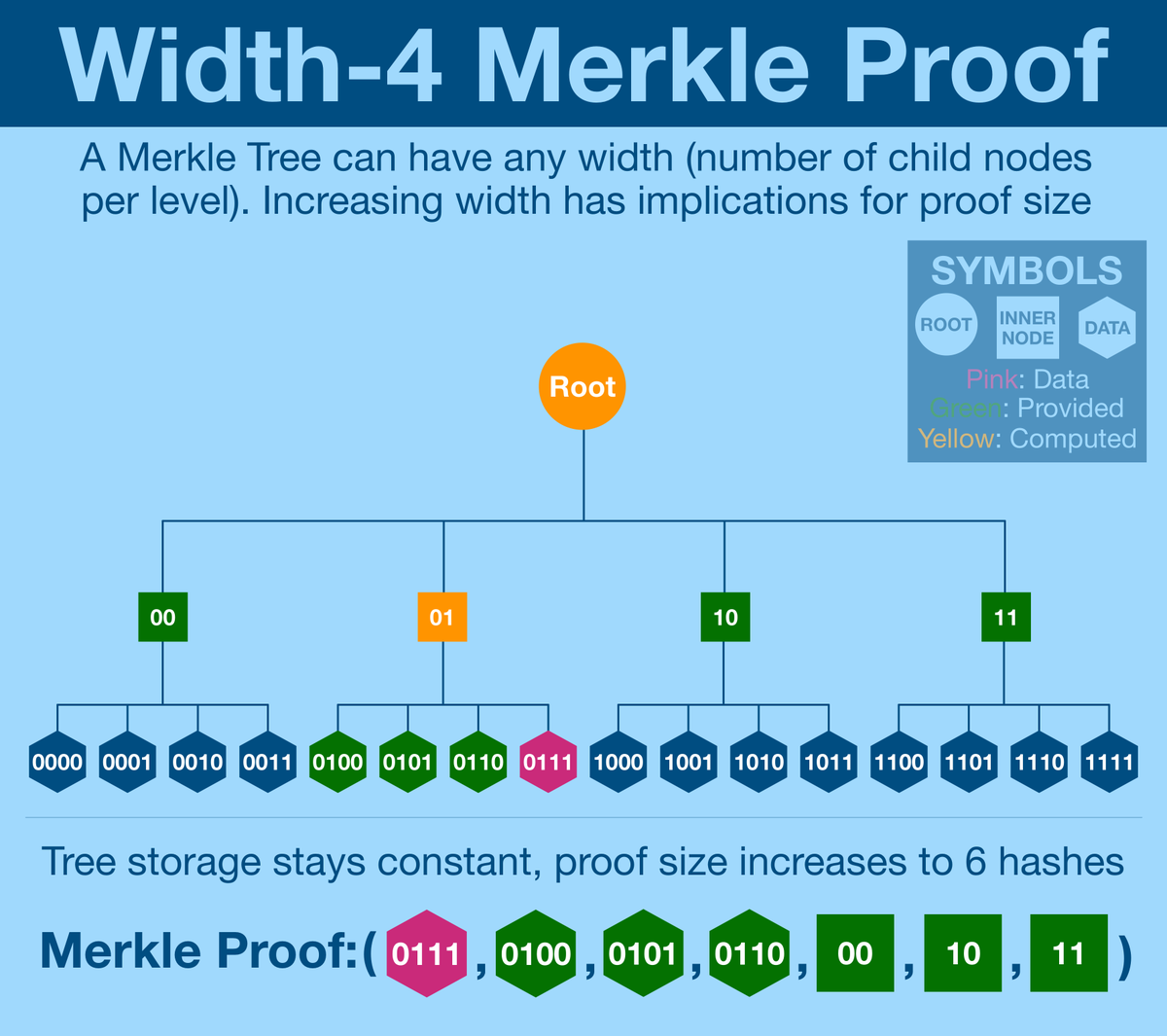
Turns out, the Merkle proof is actually LARGER.
Yes, there are less levels we need to traverse before we reach the root, but each level requires so much more data. Maybe a width of 4 is especially bad?
Unfortunately, this is not the case.
The wider a Merkle Tree gets, the less efficient the Merkle proofs are.
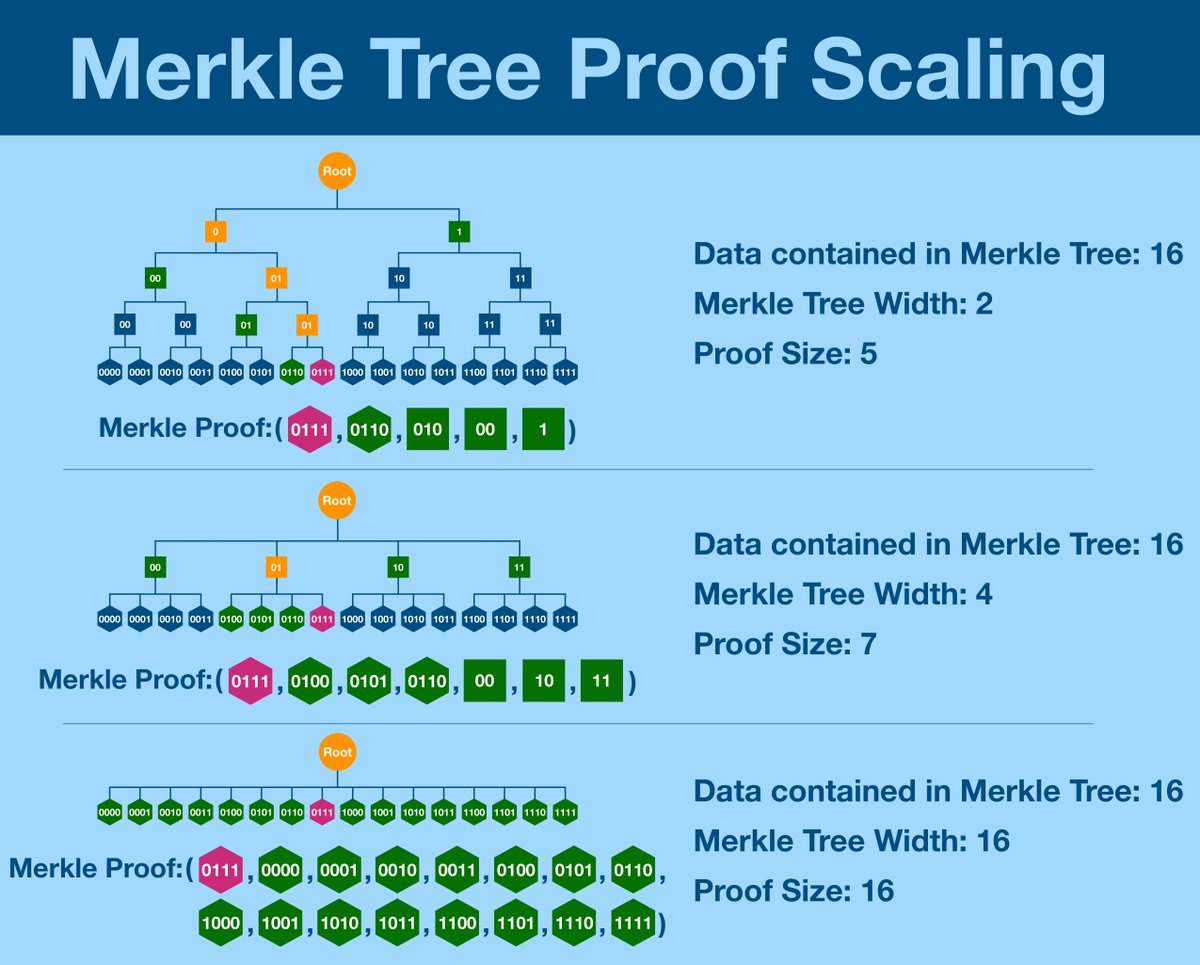
In fact, a Merkle Tree is optimal when width = 2.
Take a look at the last one, where width = 16. That's what Ethereum uses.
Here's the formula for calculating how many components a Merkle proof will need.

Once again, the end result is that Merkle Trees are optimal when width = 2.
¶ Merkle Tree Scaling
Merkle trees are incredibly powerful and versatile data structures that will continue to see use long after you and I are gone, but they are not perfect for all applications.
This is especially true as the tree grows; proof size increases with tree/dataset size.
And this is ultimately the problem we find ourselves up against.
Ethereum uses Merkle trees to store the state of the EVM. Every account, balance, asset, protocol, etc is stored inside of Merkle tree, updated with every block, every 12 seconds.
Today, the tree (technically multiple) is MASSIVE, but we are still in Ethereum's infancy.
Yes, the Merkle tree still is much more efficient that transferring the entire data set, but the Merkle proofs are getting so large we are running up against the same barriers.
As previously mentioned, today Ethereum uses Merkle trees with a width of 16.
We can make some (significant) improvements just by transitioning to the optimal Merkle structure.
But that's just a band-aid for a systemic issue, for the tree will still inexhaustibly grow.
So, dear reader, here's where I am going to leave you off: with a huge freaking problem.
The data structure at the core of Ethereum is literally not scalable, it's only going to work as long as Ethereum remains (relatively) unused.
But don't worry, we'll be back.
We haven't spent all this time just figuring out what was wrong with Merkle Trees.
We've also been working on a replacement!
¶ Resources
Source Material - Twitter Link
Source Material - PDF