¶ Merkle Trees
¶ Prerequisites
¶ Hashing
Applying a hash function takes data (of arbitrary contents and size) and reduces it to a unique, compact string.
Every input produces a unique output, even if two inputs are nearly identical.
¶ Merkle Tree
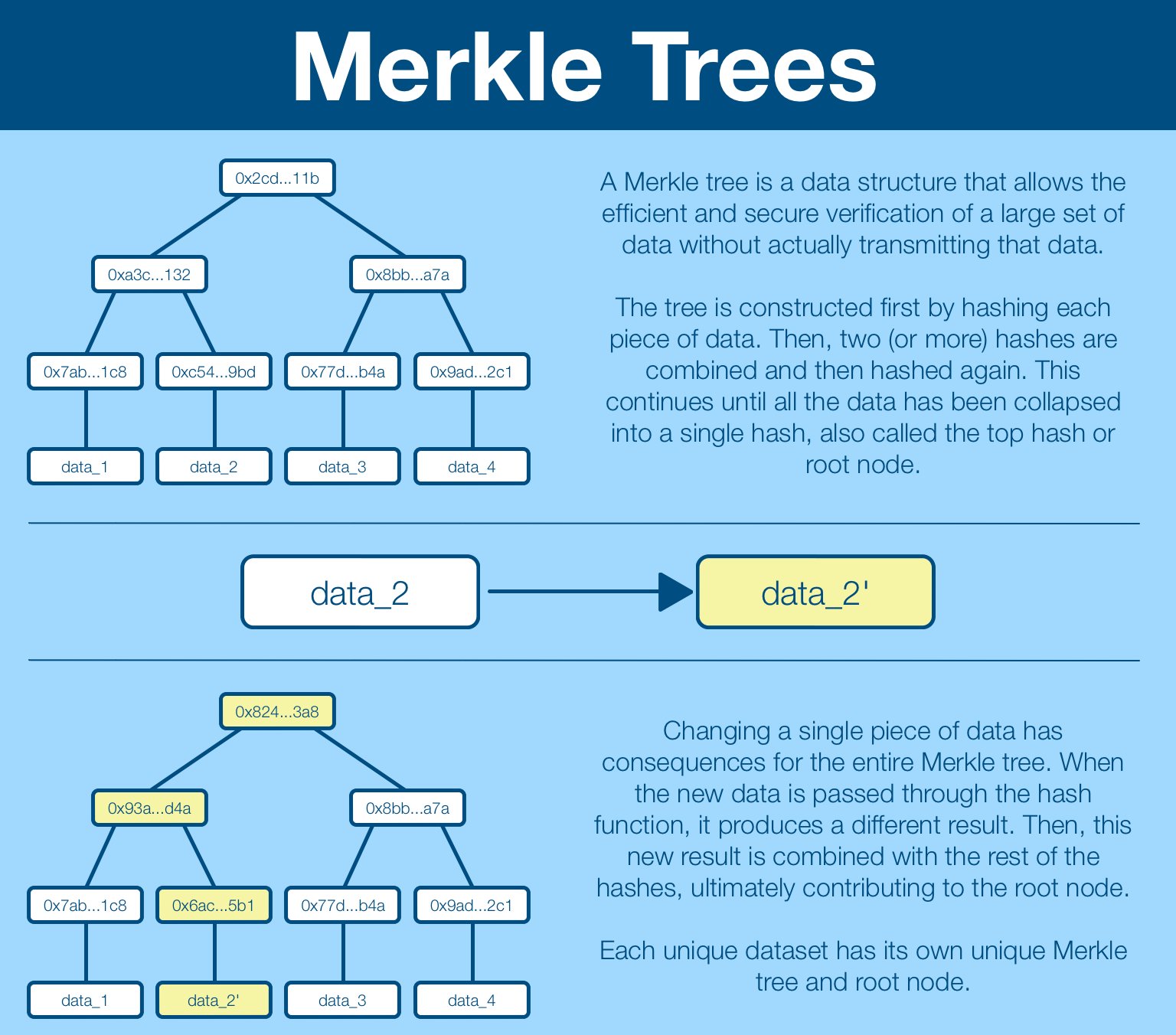
A Merkle Tree uses hashing to build a data structure that allows for quick, efficient, verifiable proof that a transaction was included in a much larger data set. Also called a hash tree, they are named after Ralph Merkle (who proposed them in 1987).
A (binary) Merkle tree is a data structure created by first applying a hash function to individual data blocks to create a list of hashes.
Then two hashes are combined and hashed again, creating a new (smaller) list of hashes.
The cycle repeats until there is a single hash.
¶ Merkle Root
The top hash (also called root hash or root node) is a single value that represents the unique structure of the Merkle tree. If any of the data is changed, the hash it creates (and all subsequent hashes) will be different, including the root node.
The output of a Merkle tree is a unique identifier for that set of data; we can use a hash tree to verify a dataset without transferring the entire dataset.
The Merkle root can be derived locally and then compared externally. If the roots match, the data sets are the same.
Because Merkle trees rely on hashing functions, they only operate in one direction: it is very easy to build a tree from raw data, but it is impossible to recover the data from the tree.
Thus, a Merkle root can be posted publicly without fear of exposing the data.
However, this has an interesting dilemma: can you confirm if an individual piece of data exists within an Merkle tree? Put another way, can a Merkle tree do anything other than verify an ENTIRE dataset?
The answer: of course!
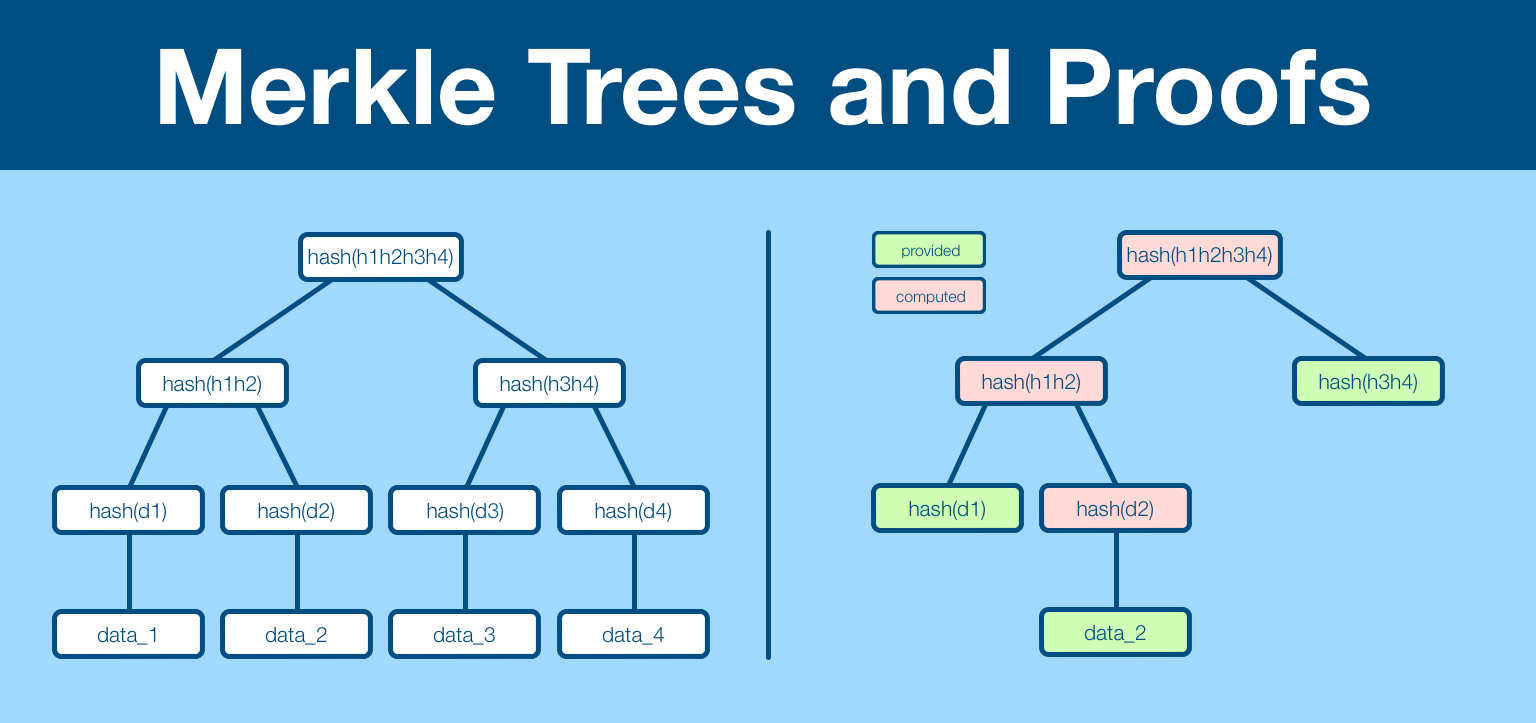
¶ Merkle Proofs
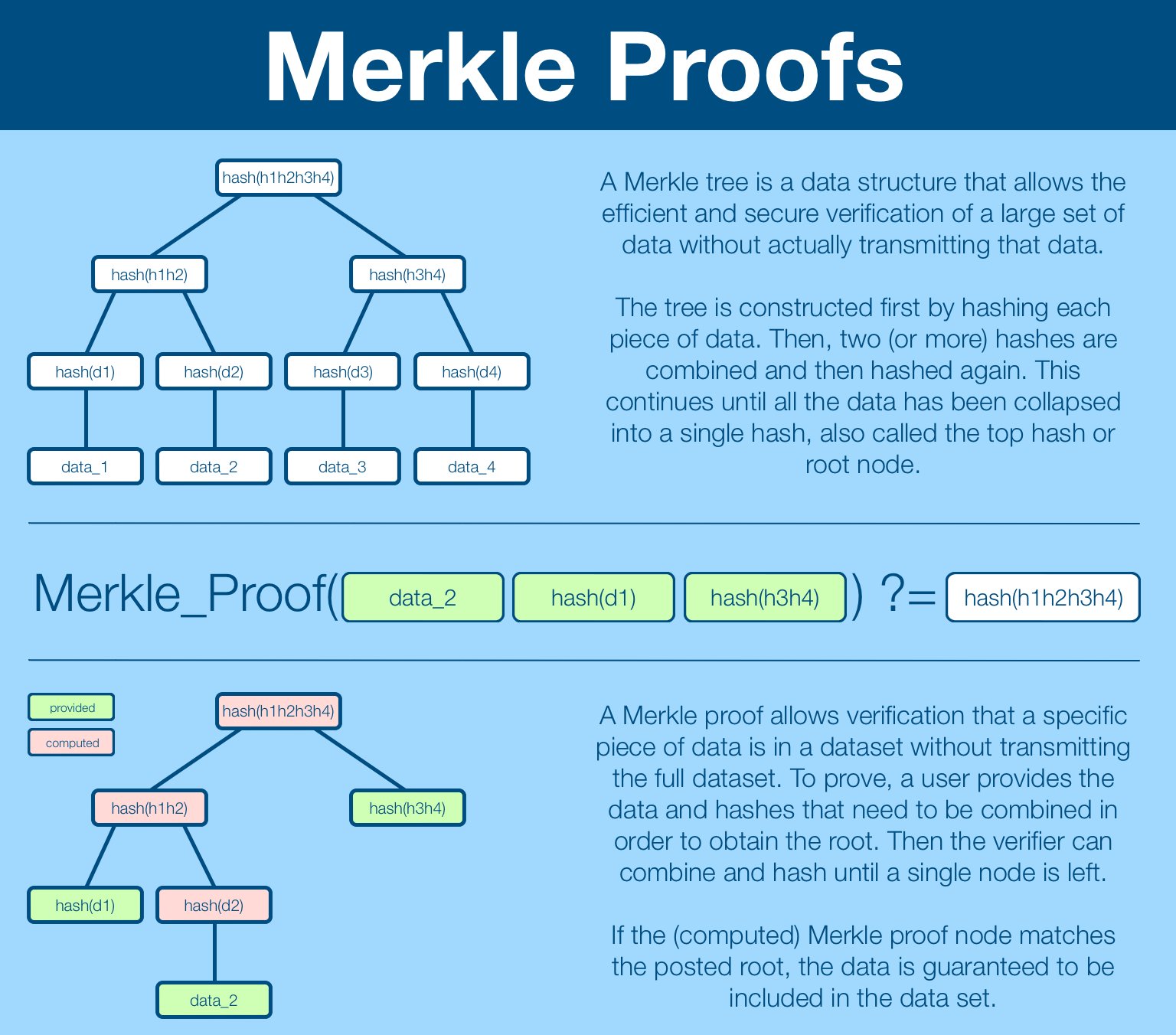
A Merkle proof is established by providing the specific data and the intermediate hashes which allow a verifier to recreate the Merkle tree. If the newly computed root node matches root node of the dataset, the verifier can be certain the data is in the dataset.
The examples above have been for datasets of size 4, in practice Merkle trees are deployed for datasets in the millions, billions and trillions.
As the dataset get larger, Merkle trees become more and more efficient. Both in coordination and verification.
Merkle trees provide a single, unique output for an an entire set of data; a multi-GB file can be reduced down to a single line. A well designed network can maintain many resources locally and coordinate by communicating an extremely lightweight root hash.
This effect could be achieved by simple hashing; a good hash function generates a a unique hash for every dataset. The Merkle proof gives us the ability to verify inclusion incredibly efficiently (for the true nerds, verification complexity scales O(log n)).
¶ Takeaway
When you see Merkle trees in the wild, remember this:
- Merkle Trees compress huge data sets into a single, encrypted line.
- Merkle Proofs can be used to efficiently verify data exists in a dataset.
¶
Resources
Source Material - Twitter Link
Source Material - PDF