This is part of a series on elliptic curve cryptography and its applications for Ethereum. This is simplified to a MINIMAL level, aiming at ~high-school math.
¶ Polynomial Commitment Scheme Trusted Setup
¶ Prerequisites
¶ Modular Arithmetic
The modulo operator (written as "mod") is the operation that finds the remainder.
- 10 / 3 = 3 with a remainder of 1 = 10 mod 3 = 1
- 14 / 6 = 2 with a remainder of 2 = 14 mod 6 = 2
- 3 / 10 = 0 with a remainder of 3 = 3 mod 10 = 3
Imagine a clock being mod 12.
¶ Elliptic Curve Cryptography
Deep Dive: Elliptic Curve Cryptography
It is very difficult to solve the elliptic curve discrete logarithm problem (that is, if you add two points over and over again using modular arithmetic, it takes A LOT of work to find out how many times you did it).
If a clock is mod 12, then consider the following question: "Alice left at 4 and arrived at 6. How many hours did she spend traveling?" 2 hours? 14 hours? 26 hours? The only way to figure it out is to start guessing.
This is the discrete logarithm problem.
¶ Elliptic Curve Foundation
Any (decent) cryptographic system has the same two part goal:
- transform data into digital-nonsense, indistinguishable from random noise
- allow specific individuals (and only those individuals) to reverse the process and recover the original data
Again, it is very hard to solve the elliptic curve discrete logarithm problem. Like "1,000s of gigabrains have been working for 30+ years/there are trillions of dollars at stake and we still just guessing" hard.
This is the property we are going to build our system out of.
We are going to start off by hiding a secret number inside an elliptic curve.
¶ A Hidden Secret
First, pick a number.
The number must be 100% random and secret. At the end of this process this number will be thrown away; it will never be known directly, it will just exist hidden in an elliptic curve.
For now, just use god mode: we are just going to assert that a single computer generates a random number S and permanently discards it at the end of this process.
In practice, we use methods based around secure multiparty computation... but we'll get to that part later.
¶ Preparing the Curve
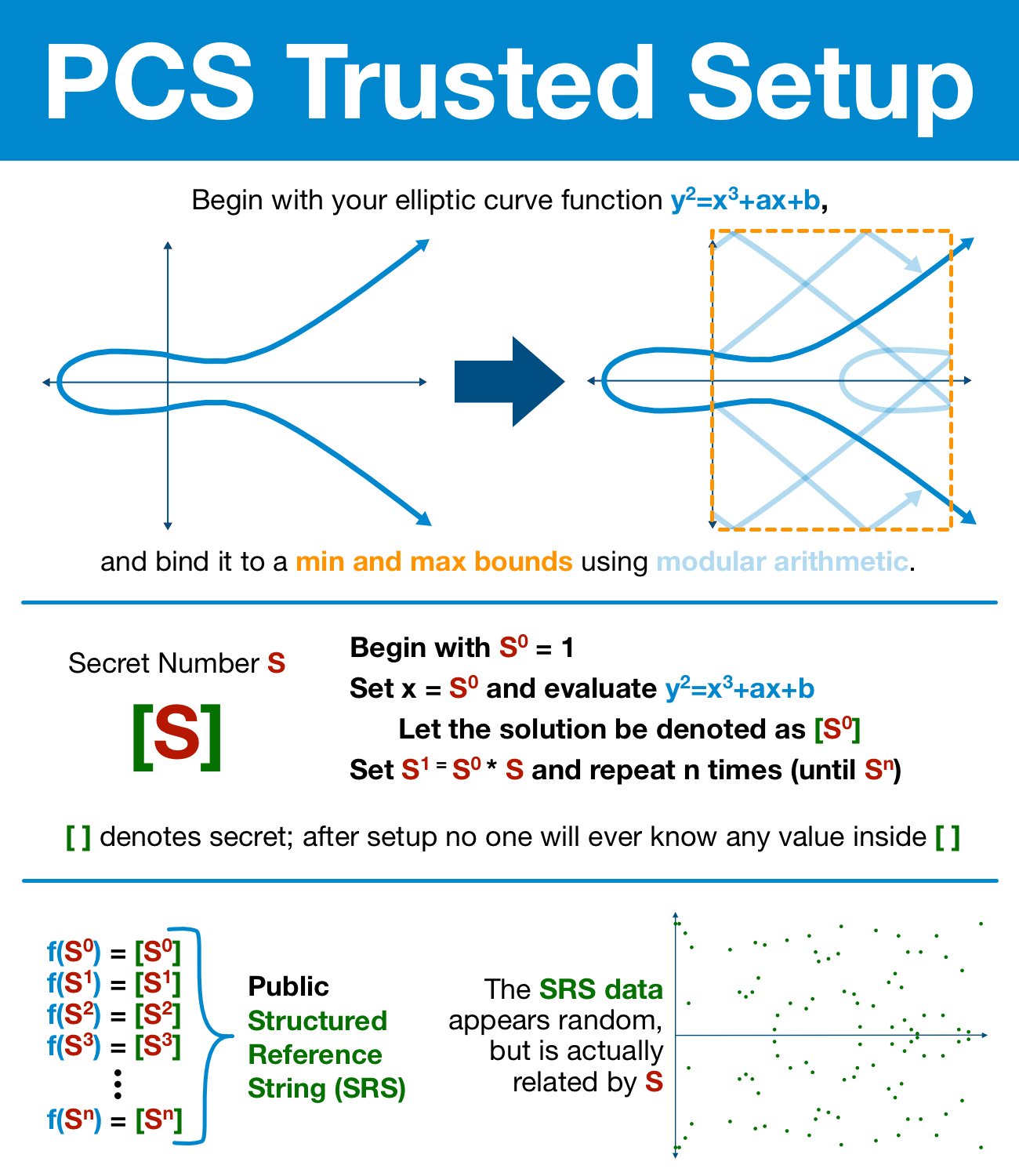
Now that we have our secret S, it's time to prepare our elliptic curve.
First, we must bind our curve to a minimum and maximum bounds using modular arithmetic. As previously discussed, this will (intentionally) introduce the elliptic curve discrete logarithm problem.
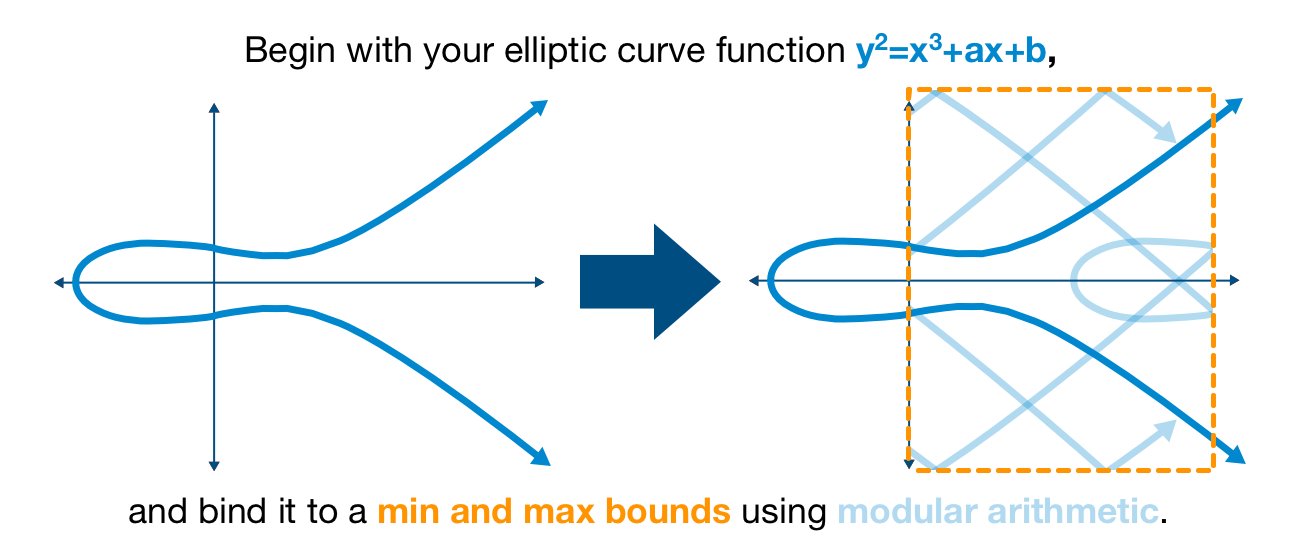
Next, we are going to use our (modular) elliptic curve and our secret (number) S to generate a series of values.
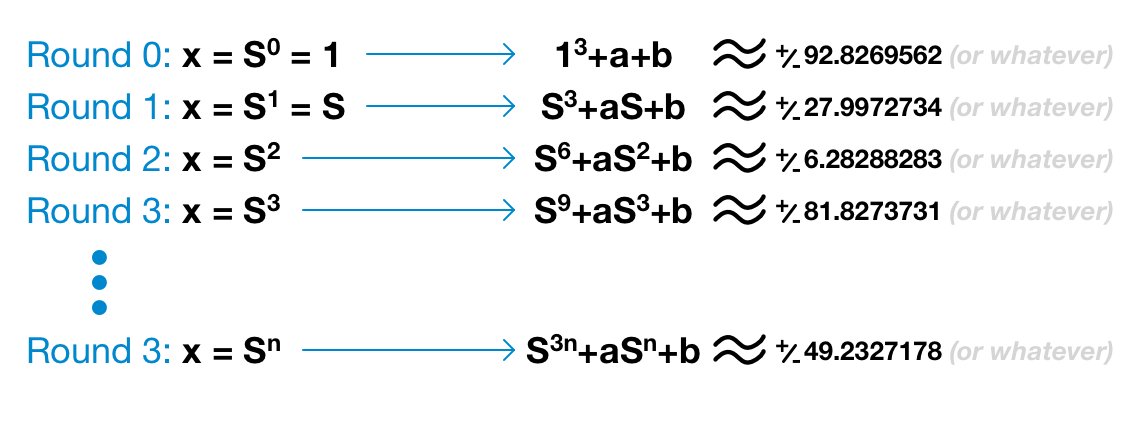
We want to start with S0 and end with Sn, each time feeding it into our elliptic curve formula and generate a new value, representing a point on the curve.
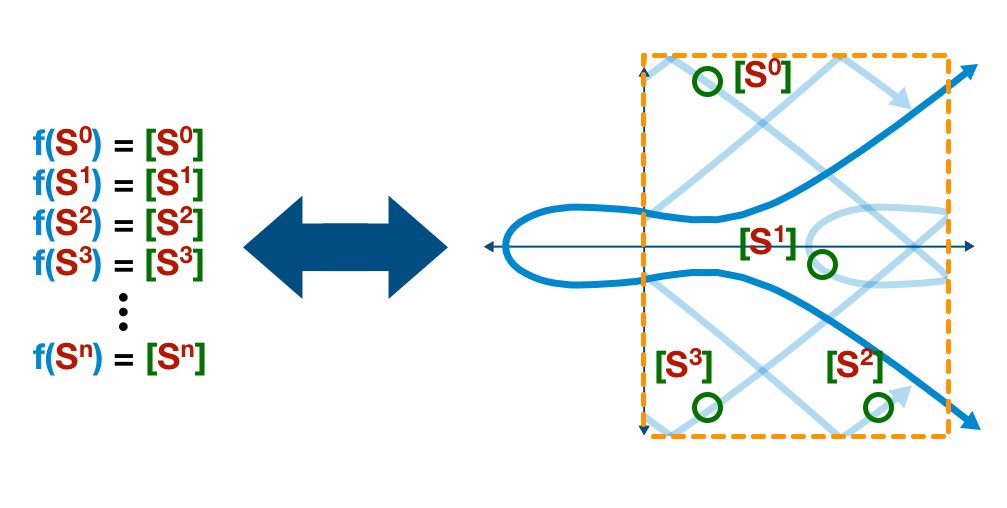
Take a look at the example below. Don't pay attention to the specific numbers (I literally bashed my keyboard like an ape).
The point is
- to illustrate how S progresses with each round
- to understand the outputs are real values/numbers, not formulas.
In fact, both parts components of the elliptic curve point (x and y) are provided - which includes S, S2, S3, etc. But this is when the discrete logarithm problem comes into play.
The difficult problem: discovering S in precisely this situation.
¶ A Lost Number

Without access to S, the list of points look like noise. Yes, we can see the clear horizontal symmetry, but otherwise it seems near random (for the record, this randomness is at the mathematical level, no need to rely on my graphic).
But that's the point! It's NOT random!
We use this process to generate n points - n is as many as we desire, we’ll understand how many we need a little later in the series.
At the end of the process we permanently discard S. After this step, the true value of S becomes forever lost.
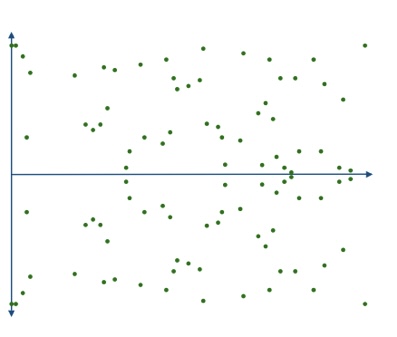
This is all that remains of S. A secret number lost in a scattered mess of points.
An arbitrary splattering of points, indistinguishable from random data.
Exactly what we are looking for in a robust cryptographic system!
¶ Summary
If nothing else, here's what you should walk away with:
- we want to hide a secret number S
- we generate points by repeatedly multiplying S with itself and applying our elliptic curve function
- the specific points - related by S - are indistinguishable from random data
- the true value of S is destroyed and lost, forever
¶ Resources
Source Material - Twitter Link
Source Material - PDF