¶ Vectors
¶ Mathematical Vectors

A vector is a concept used to convey quantities that cannot be expressed by a single number.
Think about velocity, which is a mathematician's way of saying "speed plus direction."
Speed is 10 m/s. Velocity is 10 m/s in a north-west direction.
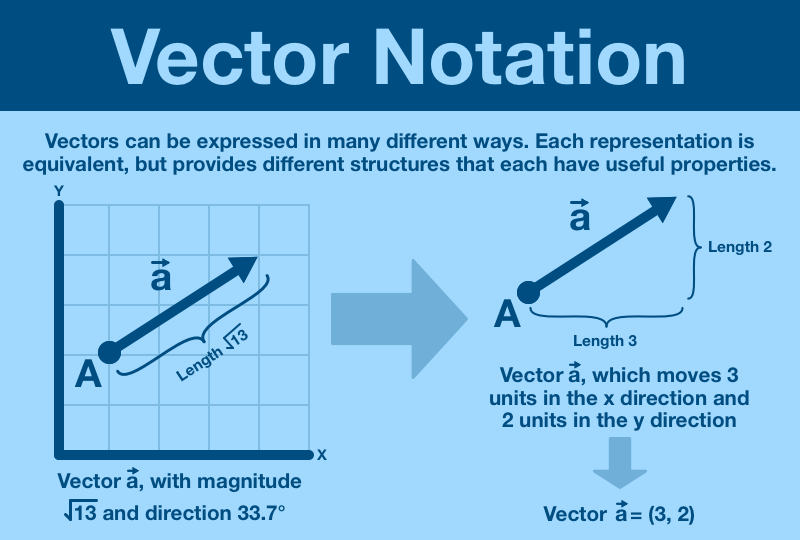
¶ Vector Notation
Vectors are incredibly versatile and show up again and again across mathematics. There are many different ways to express a vector, each having their own benefits and drawbacks.
Here are just a few of the ways we can express the same information.
¶ Multi-Dimensional Vectors
Below is an example of a 3-dimensional vector.
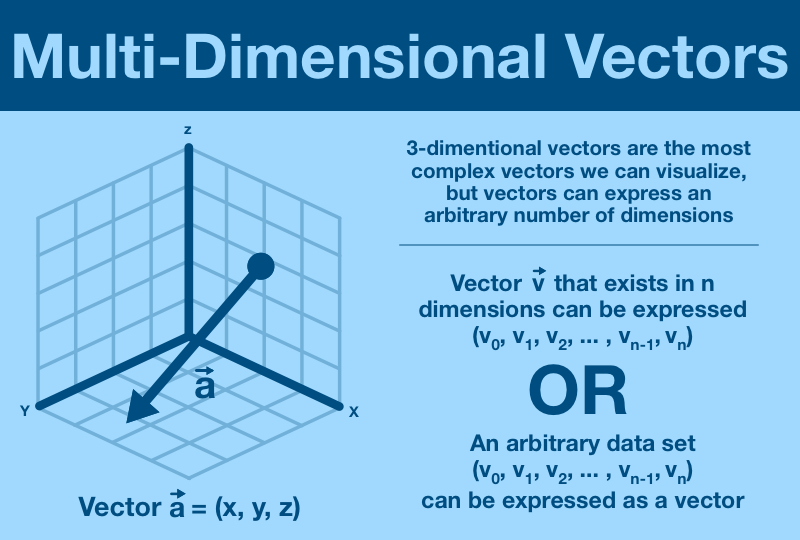
This is as far as the human brain can visualize, but mathematical dimensions can continue far beyond 3; they can go arbitrarily high.
A vector in n-dimensional space can hold up to n data points, one piece of data in each dimension.
The easiest way to see this is in the (v_0, v_1, ... , v_n) notation. Each dimension provides capacity to store an extra point of data.
Now you might be asking yourself "ok, I understand that we can put data into a vector, but why would I want to?"
Remember, vectors are mathematical primitives. They are incredibly powerful because they can be programmatically manipulated.
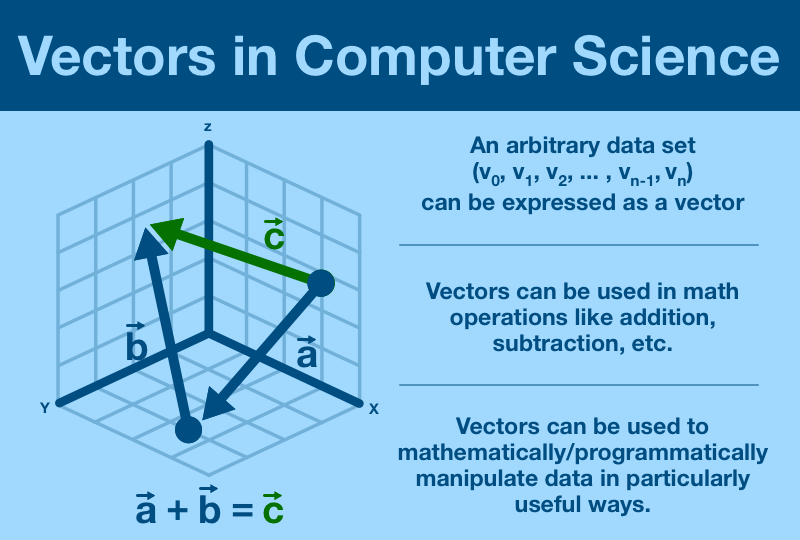
¶ Vectors in Computer Science
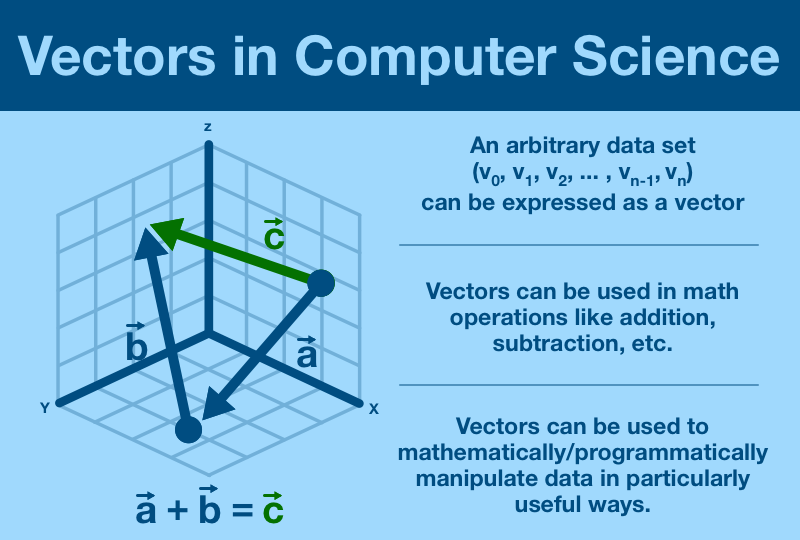
Think about 3D space, a vector just looks like an arrow.
Take two arrows, place them tip-to-tip. Draw a new arrow from the start of the first one to the end of the second.
You've just done vector addition!
This is the end of our short intro to vectors.
For now, all you need to remember is simple: vectors allow us to store an arbitrary amount of data in a way that can be mathematically manipulated.
Now let's go look at where we see them in use!
¶ Resources
Source Material - Twitter Link
Source Material - PDF