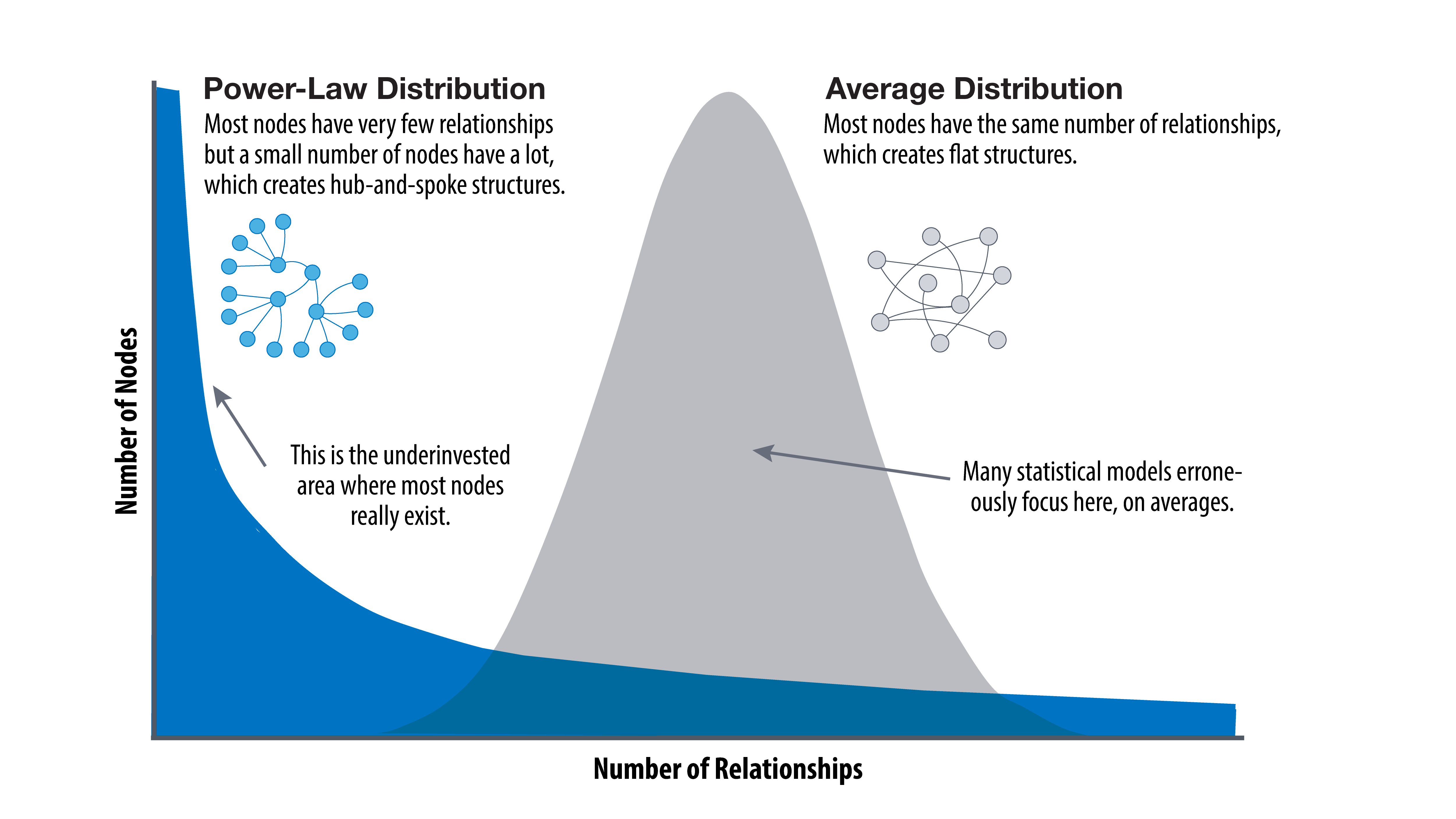
¶ Power Law
¶ Simple Example
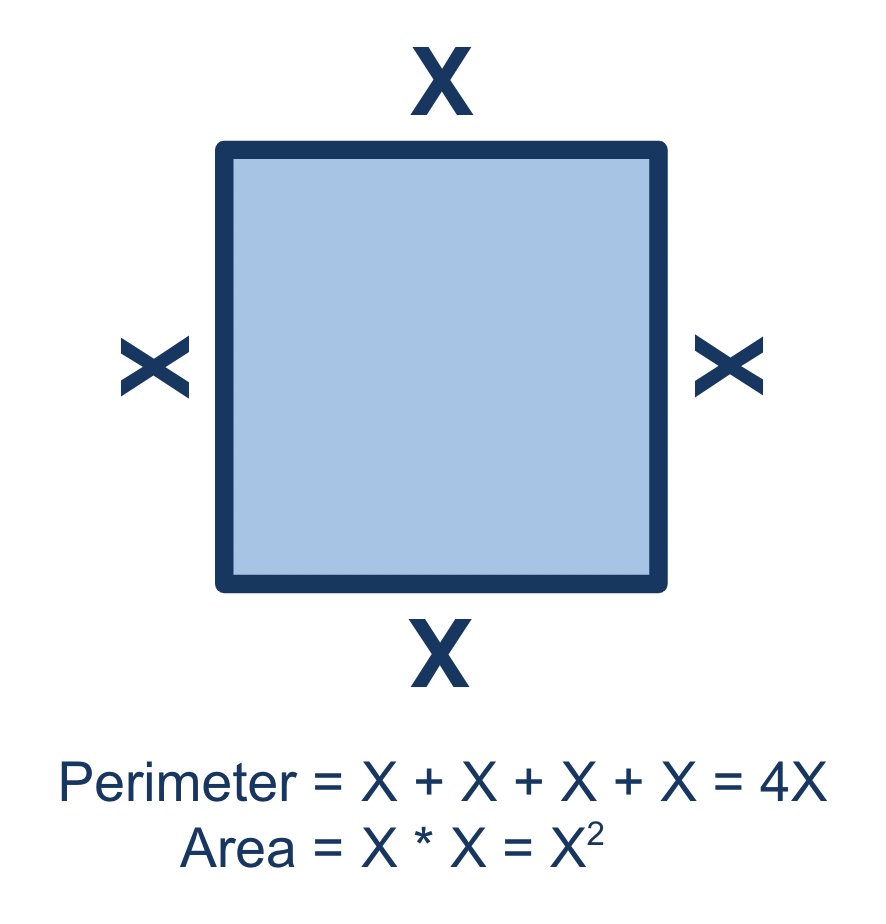
Consider a square with sides of length X. An increase in side length results in:
- the perimeter changing by a linear factor (multiplied by 4)
- the area changing by a proportional factor (multiplied by X)
The relationship of the area to side length is a power law.
¶ Definition
A Power Law relationship is one in which a change in one thing can lead to a large change in the other.
Written as an equation, a power law relationship fits this form: Y = MXᴮ, with M and B are constants. A small change in X results in a proportionally large change in Y.
¶ Linear Relationships
If B = 1, the relationship is linear.
- to double a cake recipe, you need twice as much flour
- to drive twice as far it will take twice as long.
Linear relationships, in which twice-as-big requires twice-as-much, are simple and intuitive.
¶ Nonlinear Relationships
Nonlinear relationships are more complicated; small effects can produce incredibly amplified (B > 1) or dampened (B < 1) changes in a systems.
And, fortunately or not, the universe tends to manifest as nonlinear relationships.
¶ Examples
Take, for example, Keibler's law, which states that animal’s metabolic rate increases at three-fourths of the power of the animal’s weight (mass). If a rabbit weighs one 100x as much as a mouse, the rabbit’s metabolic rate will be 32 times the mouse’s.
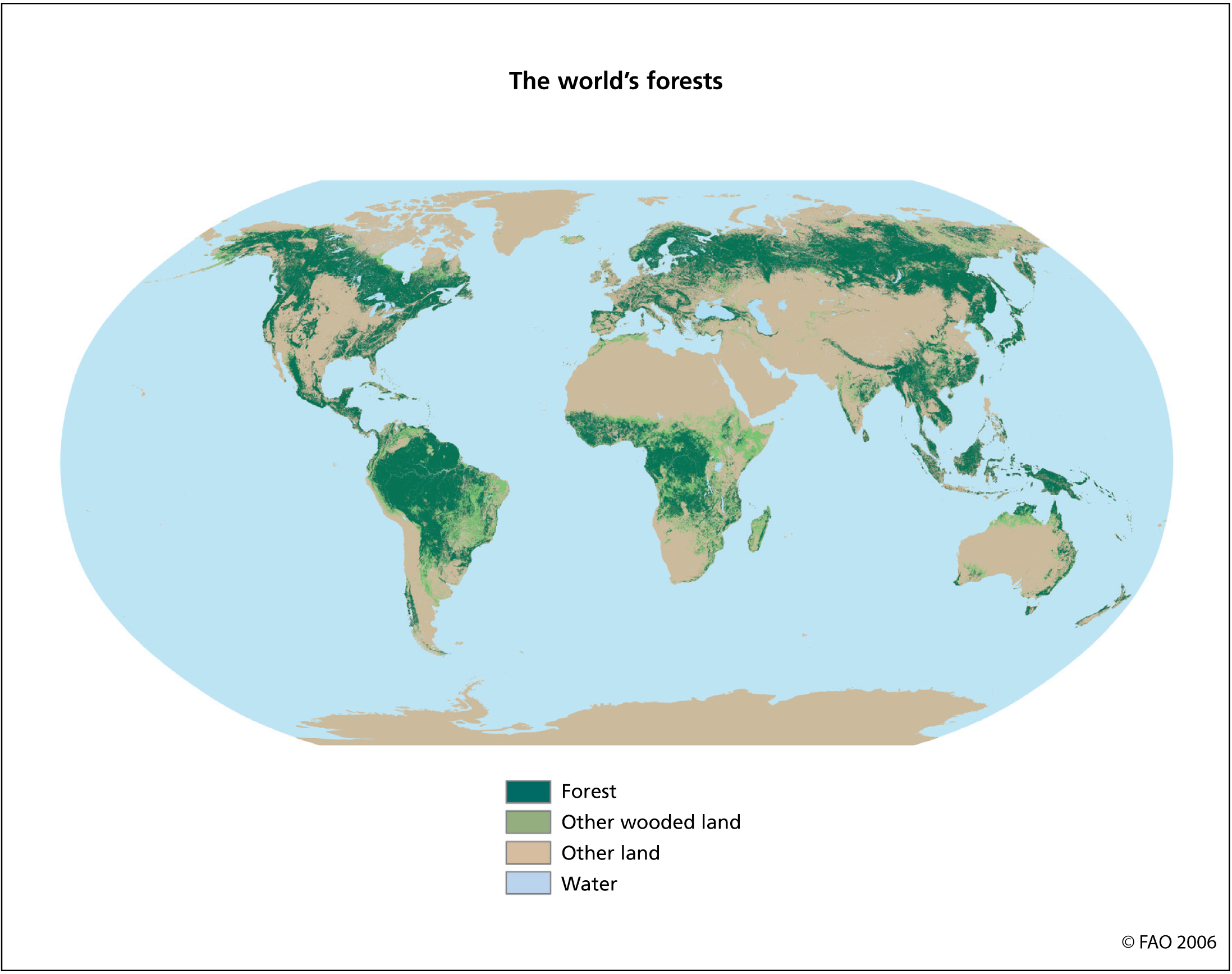
Turns out the earth's trees also follow a power law distribution: although close to one third of the planet is covered by forest, more than half (54%) of the world's forests are found in 5 countries.
¶ Pareto Principle
But if nature seems partial to power law relationships, humans are much more obsessed. Through the lens of statistics, almost everything we build ends up with a non-linear distribution: Income/wealth, internet content generation, frequency of words, city size, even wars!
In fact, this phenomena is so prevalent and important that economist have built a whole branch of study around it. But we'll just sum it up with the Pareto Principle: For many outcomes, roughly 80% of consequences come from 20% of causes.

The power law, named because exponential equations describe severely unequal distributions, is the law of the universe. It defines our surroundings so completely that we usually don’t even see it.
¶ Mathematical Models
To be clear, the power law and Pareto principal are not written rules. They are mental models that describe a huge amount of the phenomena that exists on the earth.
Each example is a consequence of specific conditions, but can be articulated by a common idea.
"All models are wrong, but some are useful."
- George Box, statistician
Even though statistical, financial or mental models always fall short of the complexities of reality, they can still be useful nonetheless.
As you continue on your crypto journey, keep an eye out for examples of power law relationships; you will find PLENTY.
¶ Resources
Further Reading: Power Laws: How Nonlinear Relationships Amplify Results
Source Material: Twitter Link
Source Material: PDF