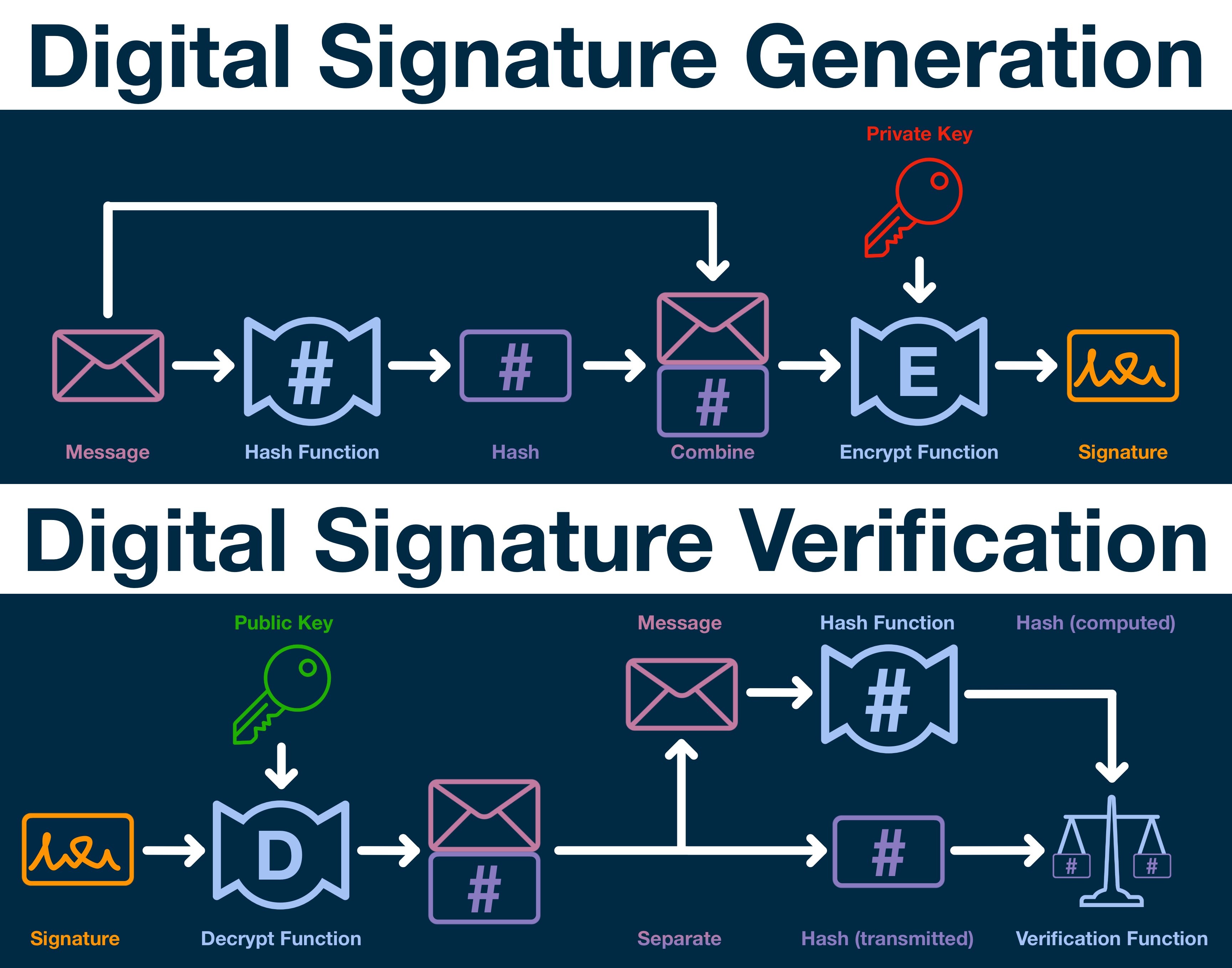
¶ Digital Signatures
¶ Prerequisites
¶ Hashing
Applying a hash function takes data (of arbitrary contents and size) and reduces it to a unique, compact string.
Every input produces a unique output, even if two inputs are nearly identical.
¶ Cryptography
Cryptography is the study of techniques to protect information so that only people can access it are those for whom the information is intended.
Encryption coverts information into a secret code that hides its true meaning; decryption moves the other way.
There are two types of encryption: symmetric and asymmetric.
- Symmetric encryption uses the same set of keys to encrypt and decrypt a message.
- Think: "Alice and Bob share a secret number (key) that they use to both encrypt and decrypt messages."
- Asymmetric encryption uses different keys for encryption and decryption.
- Think: "Alice has two keys, encryption and decryption. She shares the encryption key with anyone, who can then use it to create secret messages which can only be read with the decryption key."
¶ Shared Secrets
Asymmetric encryption is powerful because it can be used without a shared secret.
While creating a shared secret isn't that challenging (eg using Diffie-Hellman), it still requires a non-trivial amount of work. Both parties must actively interact to create the secret.
For some applications, this is ok. If you are using encryption to transfer sensitive data to your bank, it's reasonable for both parties to engage.
For others, this is a huge problem.
The reality is that both parties will not always be available to generate a secret.
¶ Digital Signatures
We are particularly concerned with a specific application of encryption: digital signatures.
A digital signature is used to publicly confirm two things:
- the message was really sent by the person claiming to send it
- the message has not been tampered with
Using a signature anyone can verify a message, even if the signatory is no longer active.
There are two industry-standard ways to create digital signatures: RSA (Rivest-Shamir-Adleman) and DSA (digital signature algorithm). Both algorithms work by the same general principle.
¶ Generating Keys
First, our cryptographic signer needs to generate both his signing and verification keys.
The signing key is used to create signatures and must remain completely PRIVATE; anyone with access can create valid signatures.
The verification key can be PUBLICly distributed.
¶ Signing a Message
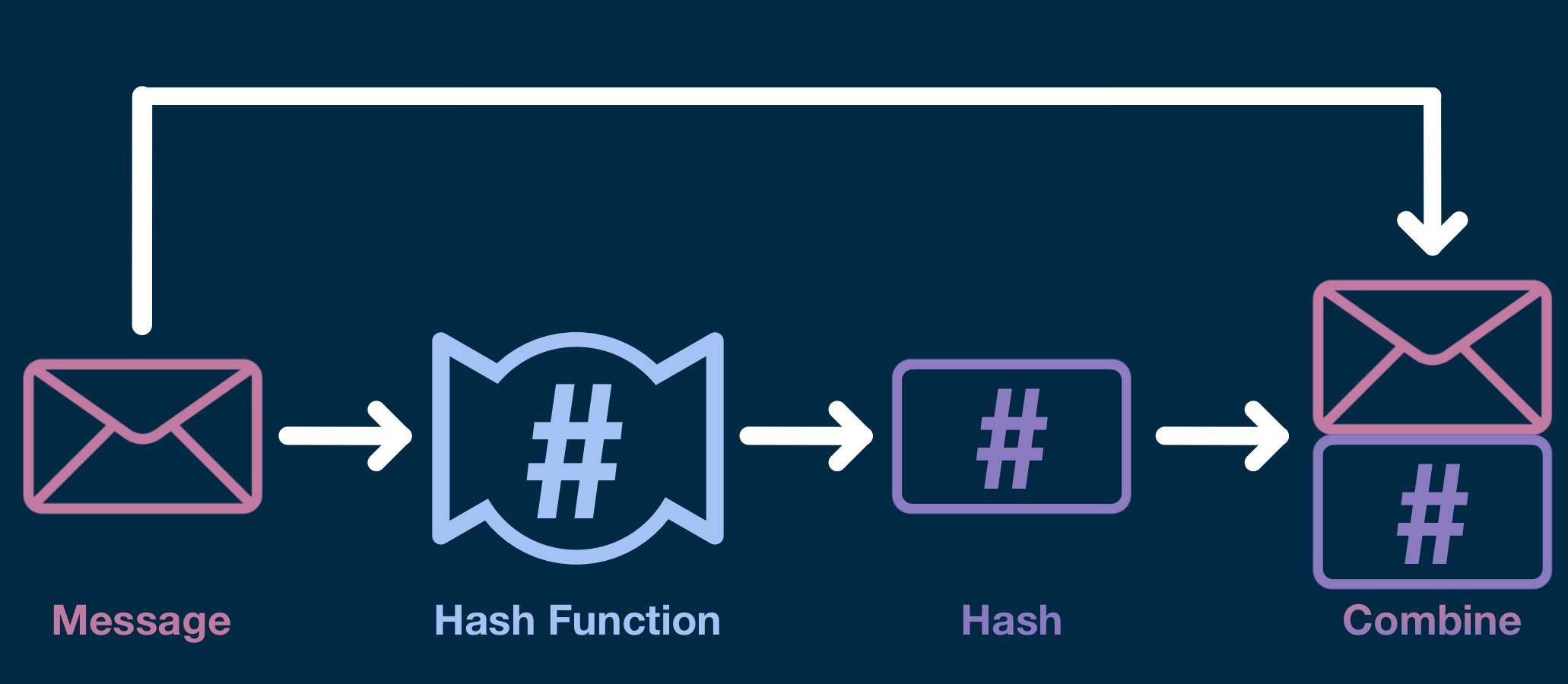
Now the signer must prepare the message for encryption/signature.
The message (the information being signed) is passed through hash function, generating a message hash. Then, the hash is appended to the end of the original message.
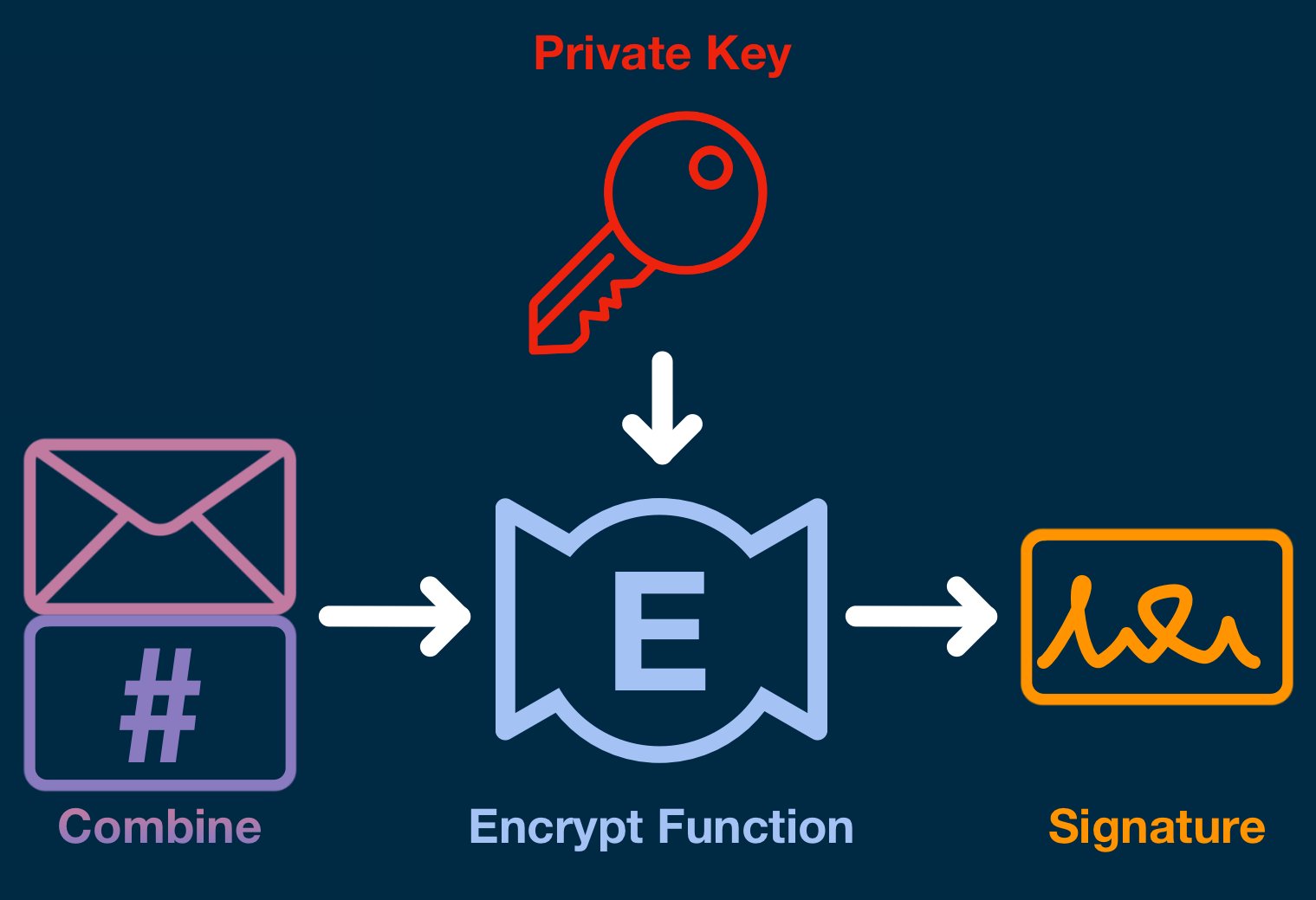
The combined message-hash and the signer's private key are fed into the encrypt function.
The encrypt function will combine both components using advanced math to create the digital signature.
The encrypt function will output the signature data, which can be freely and publicly shared. The signature will not leak any of the underlying message or private key data. It will just look like a random, meaningless chunk of data.
¶ Verifying a Signature
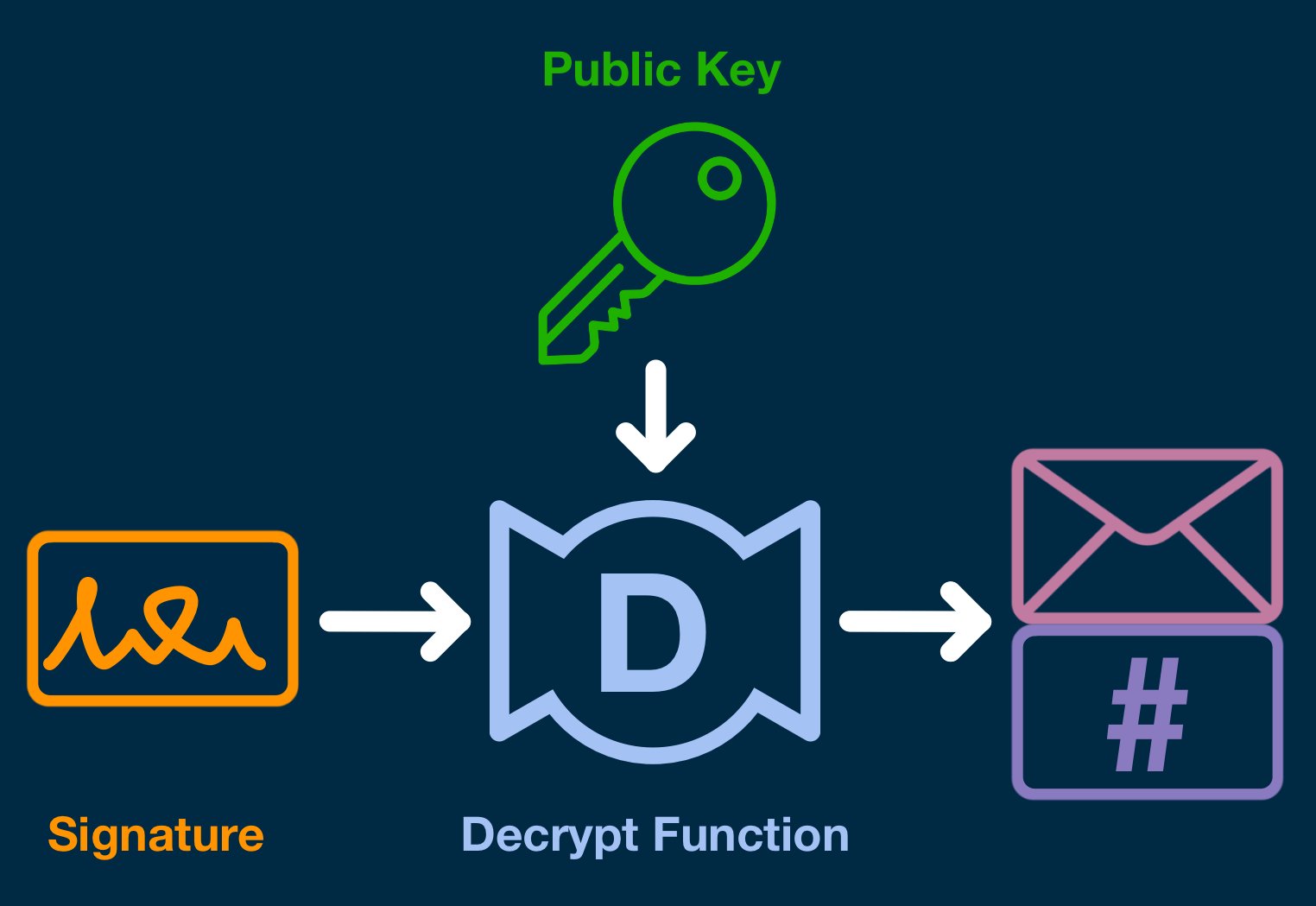
Now it is time to verify the signature.
To begin, we need to undo the encryption process, which transformed our combined message-hash into a single piece of opaque data. And so, the verifier feeds the signature and the signers public key into the decryption function.
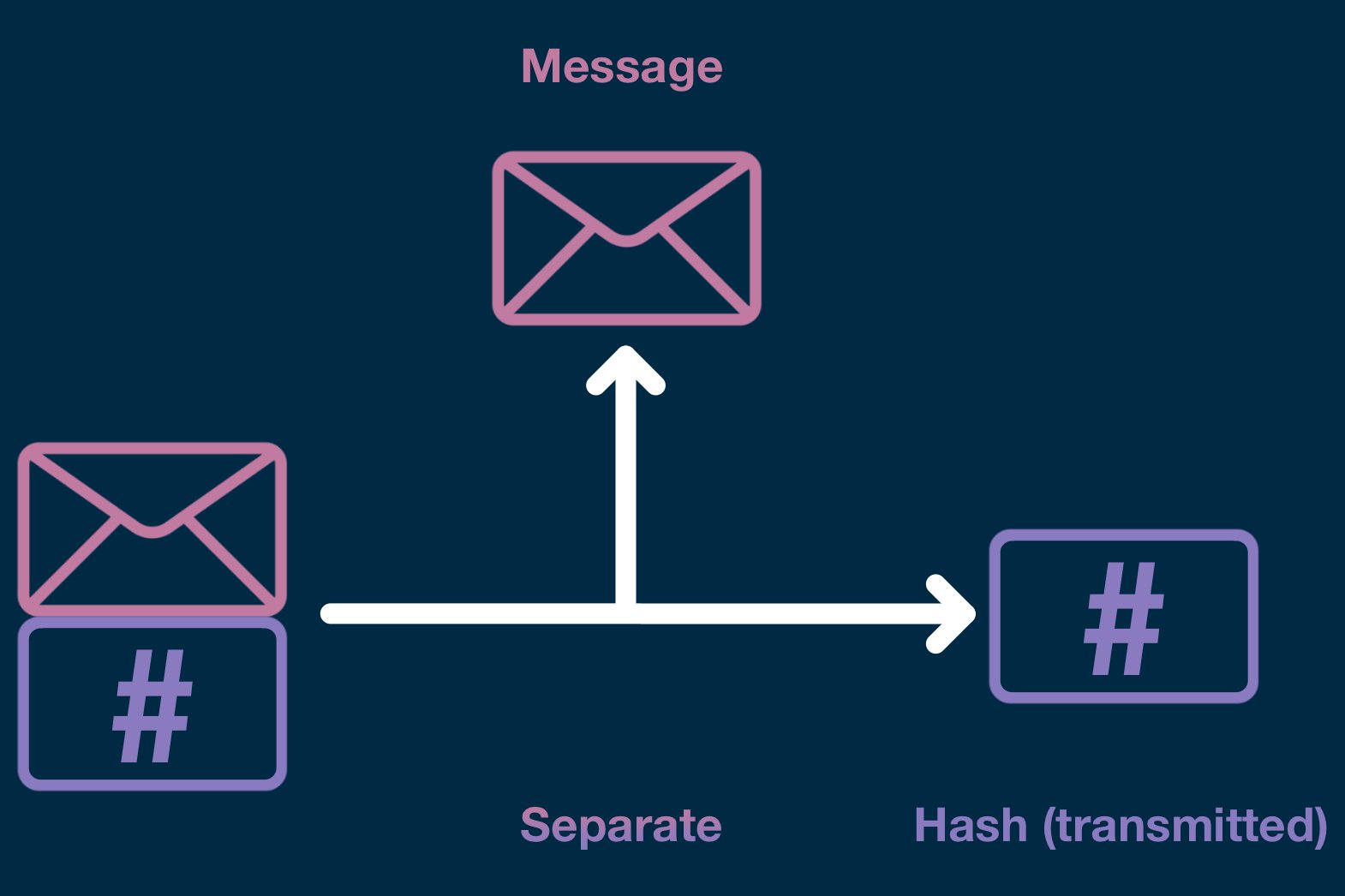
Assuming the signer created the signature with a private key that corresponds to that public key, the signature will decrypt into the same message-hash used to create the signature.
If the wrong key is used, the signature will decrypt into gibberish.
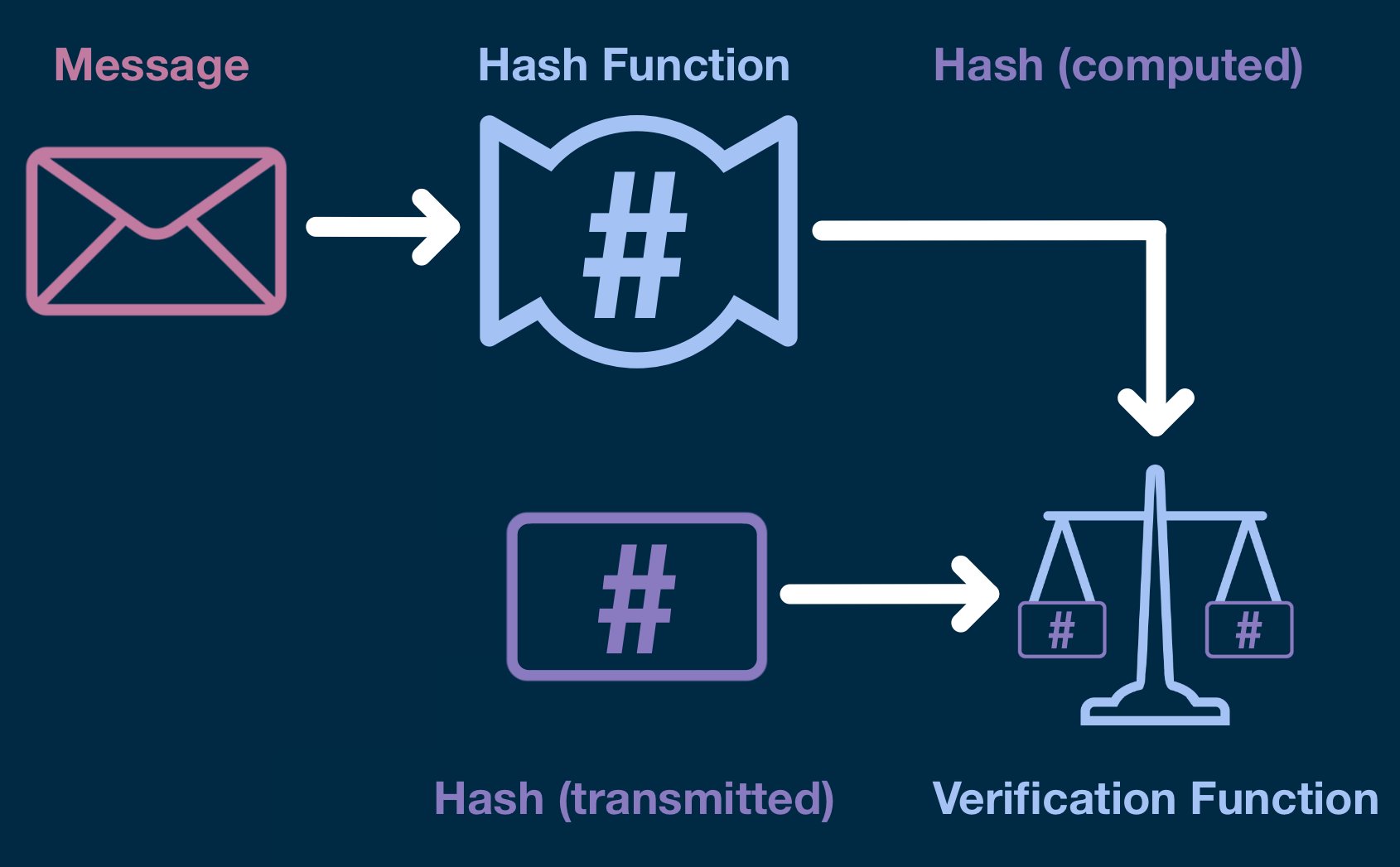
If the decryption was successful, the verifier can then pull apart the message-hash, take the message portion and run it through the hash function.
Finally, the verifier will feed this computed hash and the (decrypted) transmitted hash into the verification function.
If the message was signed by the sender who generated the public keys, the verification function will prove it to you with mathematical certainty.
¶ Authenticity and Integrity
Before we wrap, let's return to the goals of digital signatures
- the message was really sent by the person claiming to send it (authenticity)
- the message has not been tampered with (integrity)
Now let's take a second look at digital signature verification, this time as a two-step process.
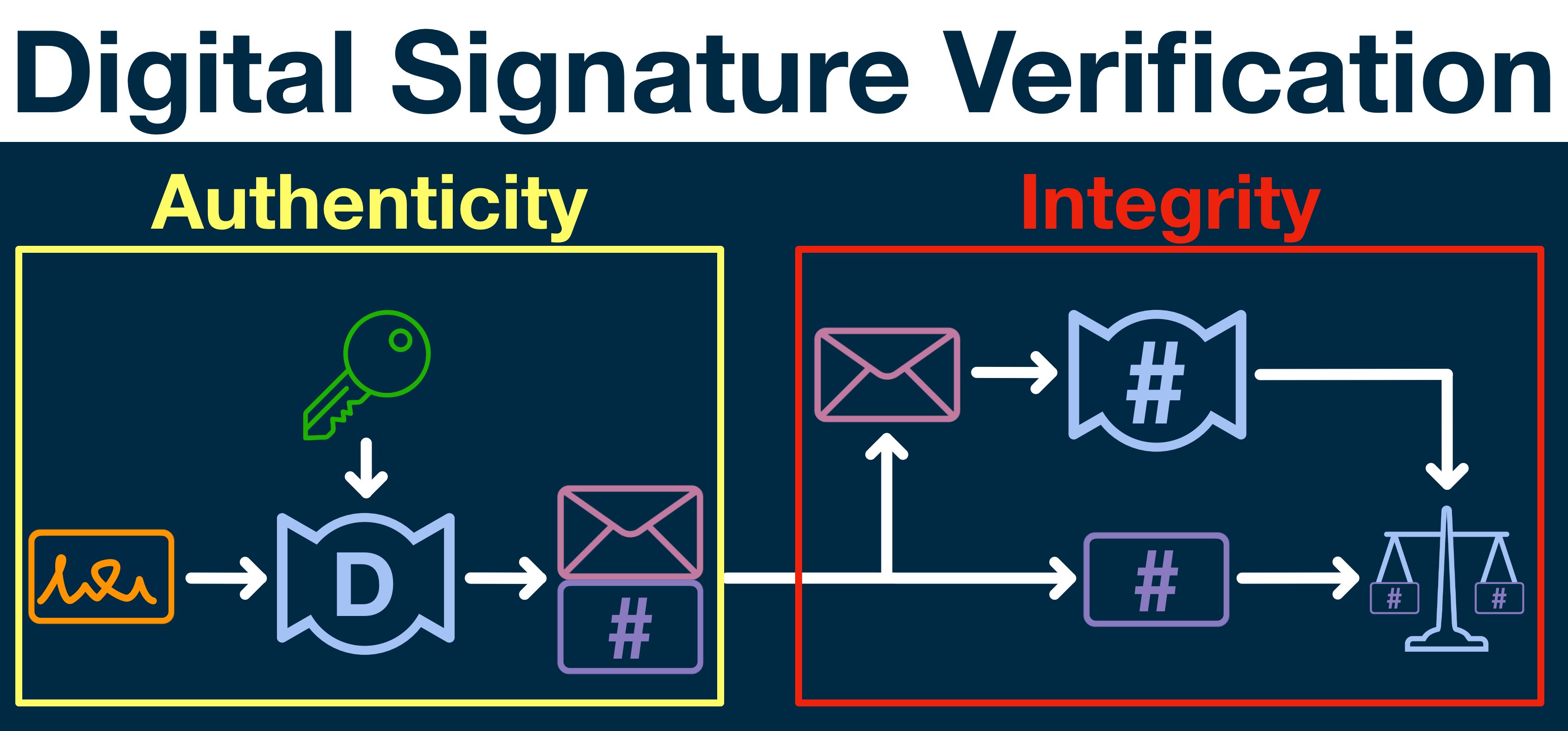
First, we decrypt the signature - only possible if we have the correct public key.
Second, we confirm the message is correct - only possible if the message matches the hash.
¶ RSA vs DSA
Finally, a few words on implementation. As previously mentioned, there are two main digital signature algorithms: RSA and DSA.
Both are considered mathematically safe, but DSA is faster at decrypting and signing, while RSA is faster at encrypting and verifying. The differences appear (mostly) in the encrypt, decrypt and verification function.
But, in general, all digital signature schemes follow the basic principles outlined in this thread.
¶ Resources
This article combines the work of 2 tweet threads:
- Digital Signatures
- Source Material - Twitter Link
- Source Material - PDF
- Digital Signatures
- Source Material - Twitter Link
- Source Material - PDF