¶ Byzantine Fault Tolerance
The Byzantine Generals Problem was introduced by an academic paper in 1982. It describes a game theory problem that shows how difficult it can be for dispersed parties to reach an agreement (consensus) without help of a trusted central party.
¶ City at War

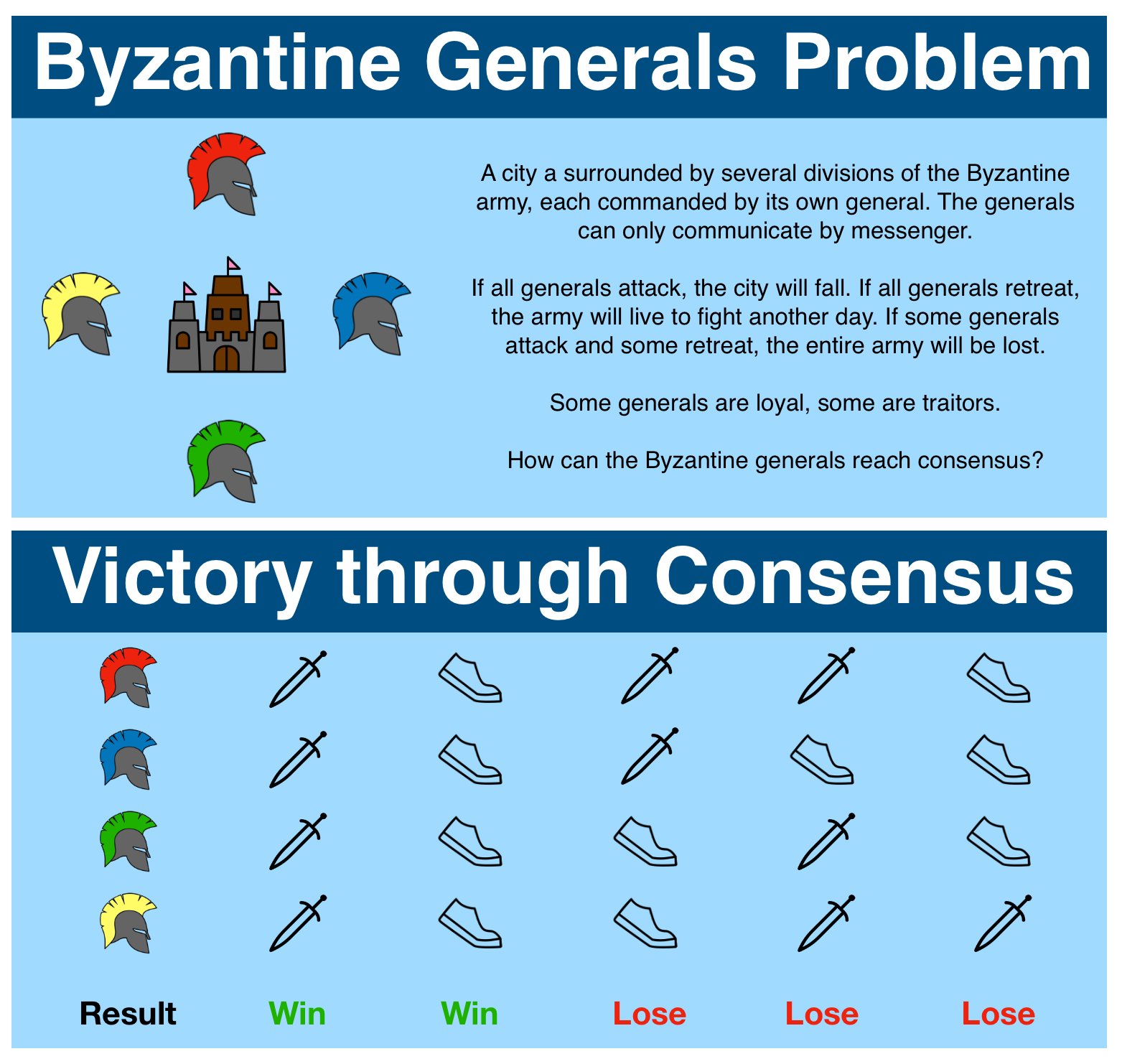
The Byzantine Generals Problem is a thought experiment: imagine an ancient city at war with Byzantium.
The city is approached from all sides by 4 division of the Byzantine army. Each division has a general with unitary control over their division.
The city is well defended; it will require the entire Byzantine army to capture it. If a single division (or a subset) attack, they will surely be defeated.
After the generals arrive and make camp for the night, they must make a choice: tomorrow, will I fight or retreat?
¶ Victory Conditions
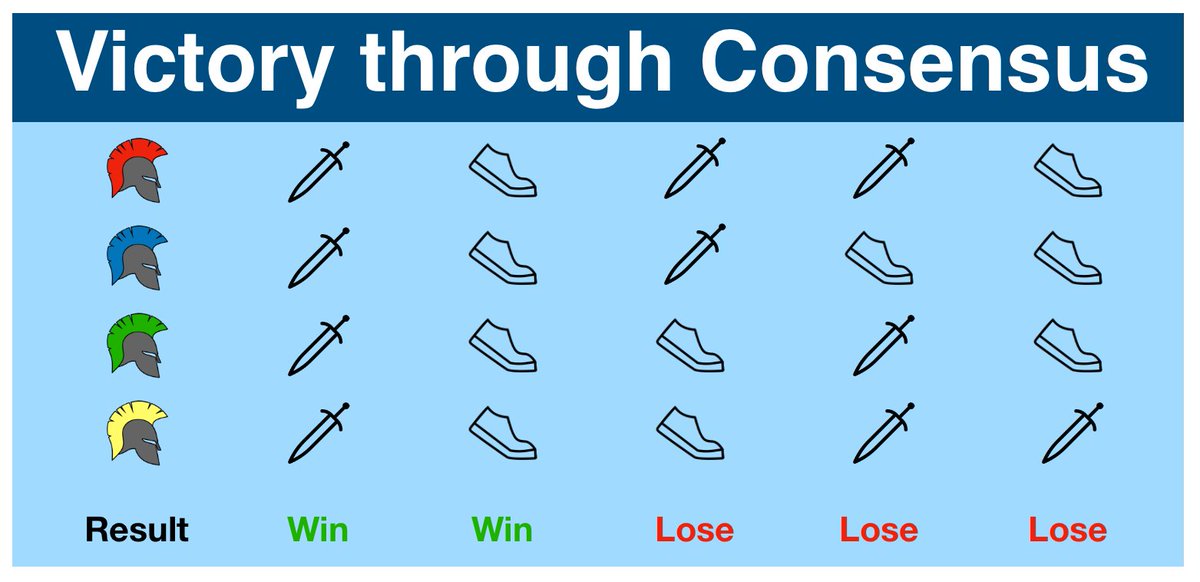
Retreat entails an orderly withdrawal of your troops; it DOES NOT mean defeat.
Defeat is attacking the city and losing the fight. Or letting your fellow general attack (and lose) while you retreat.
All that matters is the generals act in unison.
¶ The Problem with Communication
Because this is ancient times, the generals have limited communication capabilities. All they can do is write a message on a piece of paper, give it to a messenger and send them to another general.
Communication is asynchronous, bidirectional and uncoordinated.
In a perfect world, we could devise a relatively simple scheme. Maybe one general is elected a leader and sends out orders. Or maybe each general ranks their choices and the choice with the most votes wins...
...but this isn't a perfect world.
Remember, the Byzantine army is attacking a city... full of people... people who presumably don't want to Byzantine army to win.
And so, they can disrupt communications.
Imagine a world in which the people of the city keep a very close eye out for the messengers moving between generals. What if they are able to capture a messenger and stop the message?
Or what if they capture the messenger and REPLACE the message?
Maybe the people of the city have seen this invasion coming for months and have been planning sabotage the entire time. What if they were able to turn one of the Byzantine generals?
This is the core of the Byzantine Generals Problem: how can members of a network agree on a specific reality when no one can verify the identities of other members?
¶ Byzantine Fault Tolerance
A Byzantine Fault describes a system with components that may fail but does not provide clear, reliable data on whether the component has failed. A message being replaced by the city defenders or a traitorous general lying are examples of Byzantine faults.
A system that is Byzantine Fault Tolerant (BFT) is a system that is capable of resisting this class of failures (and attacks).
The Byzantine Generals’ Problem has more than one possible solution; thus, there are many possible BFT systems.
BFT systems (generally) try to optimize for two properties:
- Safety - all honest participants can agree on the sequence of events and therefore have the same information
- Liveness - the system must be able to eventually come to consensus and progress forward
¶ A Practical Solutions
A huge breakthrough came in 1999 with the publication of "Practical Byzantine Fault Tolerance" (pBFT).
pBFT is "practical" meaning that it works in asynchronous environments (like the thought experiment... or the Internet) and is relatively fast.
The pBFT algorithm provides safety and liveness assuming at least 2/3 + 1 nodes are honest.
No BFT system can support networks with more than 1/3 faulty nodes. This is a mathematical property:

¶ pBFT from 30k Feet
pBFT is complicated enough that it deserves it own deep dive.
For now, pBFT works in a series of rounds.
First a leader is chosen who then broadcasts the action to the group.
This is the typical diagram you will see; IMO it's pretty inaccessible.
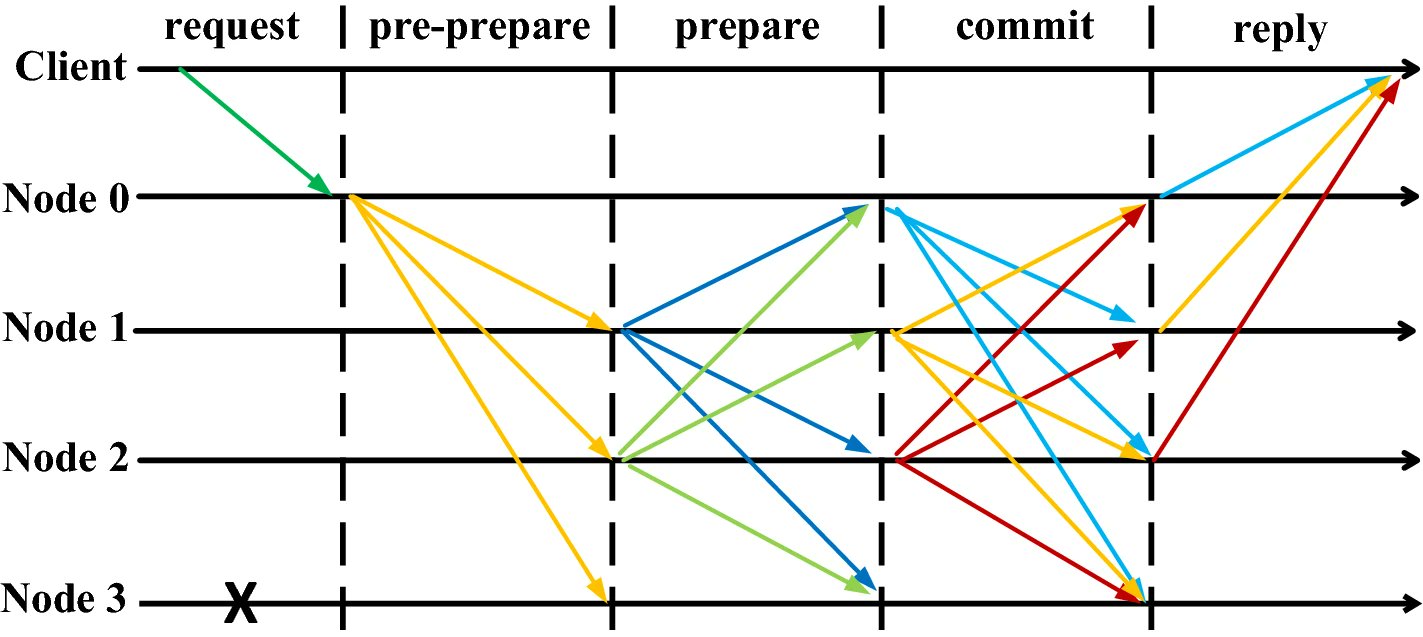
- Node 0 is the leader, who broadcasts the action to the rest of the group (pre-prepare).
- Then each member of the group broadcasts its received message to all other members (prepare).
- Once each member has received the prepare messages, they then actually do the action.
- Finally, they broadcast confirmation that they did the action (commit).
It is this two round system that gives pBFT its Byzantine fault-tolerance.
The original implementation also accounted for a faulty leader, however the process for detecting/replacing the leader (known as a "view change") was not scalable.
Nevertheless, its contribution is incalculable. In fact, it still lies at the basis of (most) Proof of Stake
¶ Byzantine Solutions
Just remember... the Byzantine Generals Problems has many solutions.
Those that look like pBFT are only one category of BFT systems; others look very different.
Some might discard voting entirely. For example, maybe use some other type of work...
¶ Resources
Source Material - Twitter Link
Source Material - PDF