This is part of a series on elliptic curve cryptography and its applications for Ethereum. This is simplified to a MINIMAL level, aiming at ~high-school math.
¶ Elliptic Curve Pairings
¶ Prerequisites
¶ Modular Arithmetic
The modulo operator (written as "mod") is the operation that finds the remainder.
- 10 / 3 = 3 with a remainder of 1 = 10 mod 3 = 1
- 14 / 6 = 2 with a remainder of 2 = 14 mod 6 = 2
- 3 / 10 = 0 with a remainder of 3 = 3 mod 10 = 3
Imagine a clock being mod 12.
¶ Elliptic Curve Cryptography
Deep Dive: Elliptic Curve Cryptography
It is very difficult to solve the elliptic curve discrete logarithm problem (that is, if you add two points over and over again using modular arithmetic, it takes A LOT of work to find out how many times you did it).
If a clock is mod 12, then consider the following question: "Alice left at 4 and arrived at 6. How many hours did she spend traveling?" 2 hours? 14 hours? 26 hours? The only way to figure it out is to start guessing.
This is the discrete logarithm problem.
¶ Vitalik's Commentary
If you've gotten this far, you know how ridiculously difficult the math has already been. I would call it pretty far beyond advanced, right?
I literally laughed out loud when I got to this part in Vitalik's blog, how did you react?

Ok we'll start small: functions.
¶ Functions
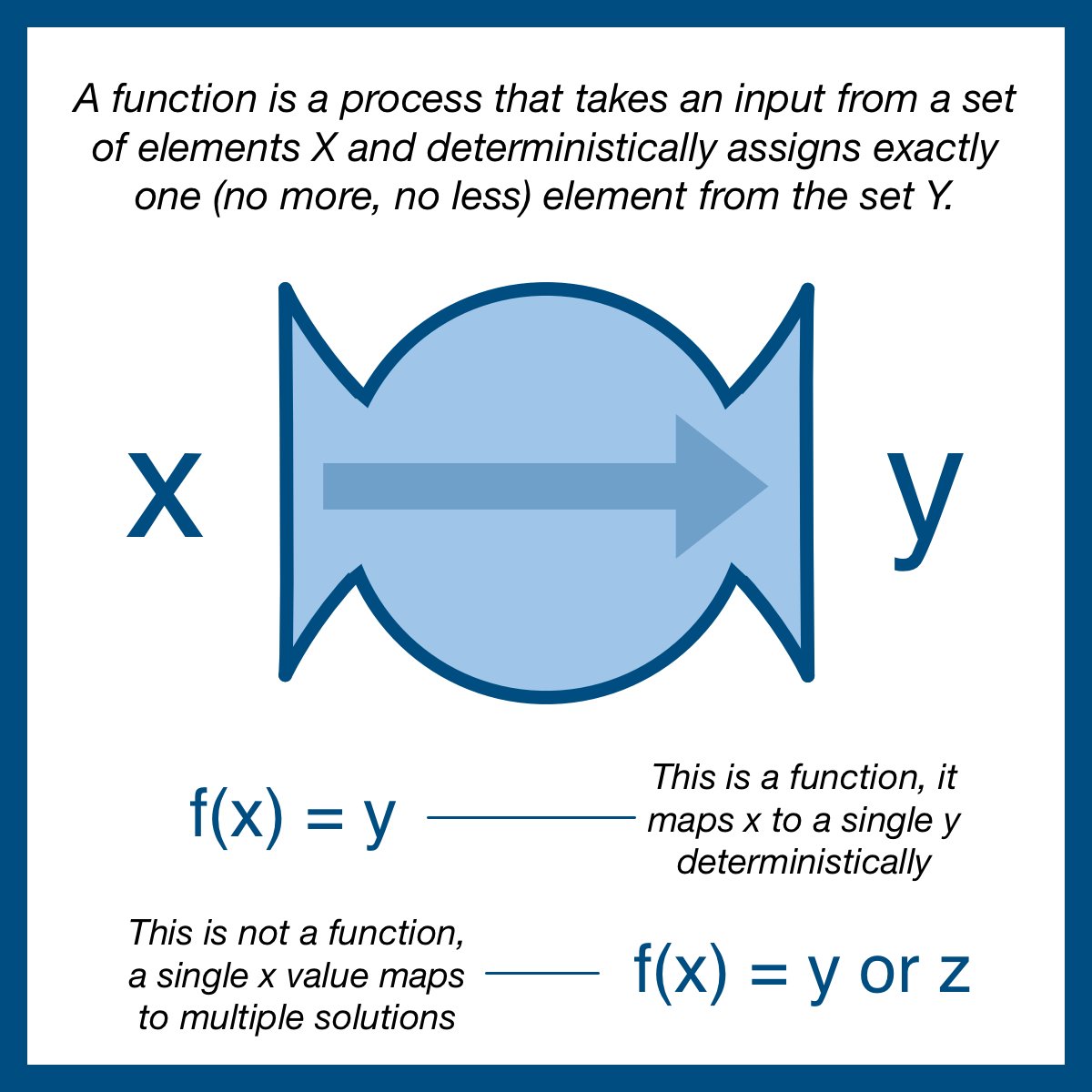
A function is a process that takes an input from a set of elements X and deterministically assigns exactly one (no more, no less) element from the set Y.
We write a function as f(x) = y; the function f, when applied to x, produces y.
¶ Sets
Functions might be familiar, the term "set" might be new. A set is simply a collection of different things:
- Set of all integers (infinite): {..., 0, 1, 2, 3... }
- Set of even integers (infinite): {..., 2, 4, 6, 8... }
- Set of Haym's favorite numbers (finite): {4, 13}
Mathematical sets and set theory is an incredibly important area of math; but we aren't really here to discuss sets.
For our purposes we just need to understand that functions can move from an input set to a different output set.
¶ One-Way Functions
If an output set/group is different from an input set/group, we gain a very specific property: the output of this kind of function cannot be used as an input.
Put another way, you can only execute these kinds of functions one time; you cannot execute them repeatedly.
This property is incredibly important for cryptology; it breaks most efficient methods of cracking crypto schemes and forces an attacker to use the slow difficult method: guess and check.
So, let's build an elliptic curve pairing!
¶ Elliptic Curve Pairings

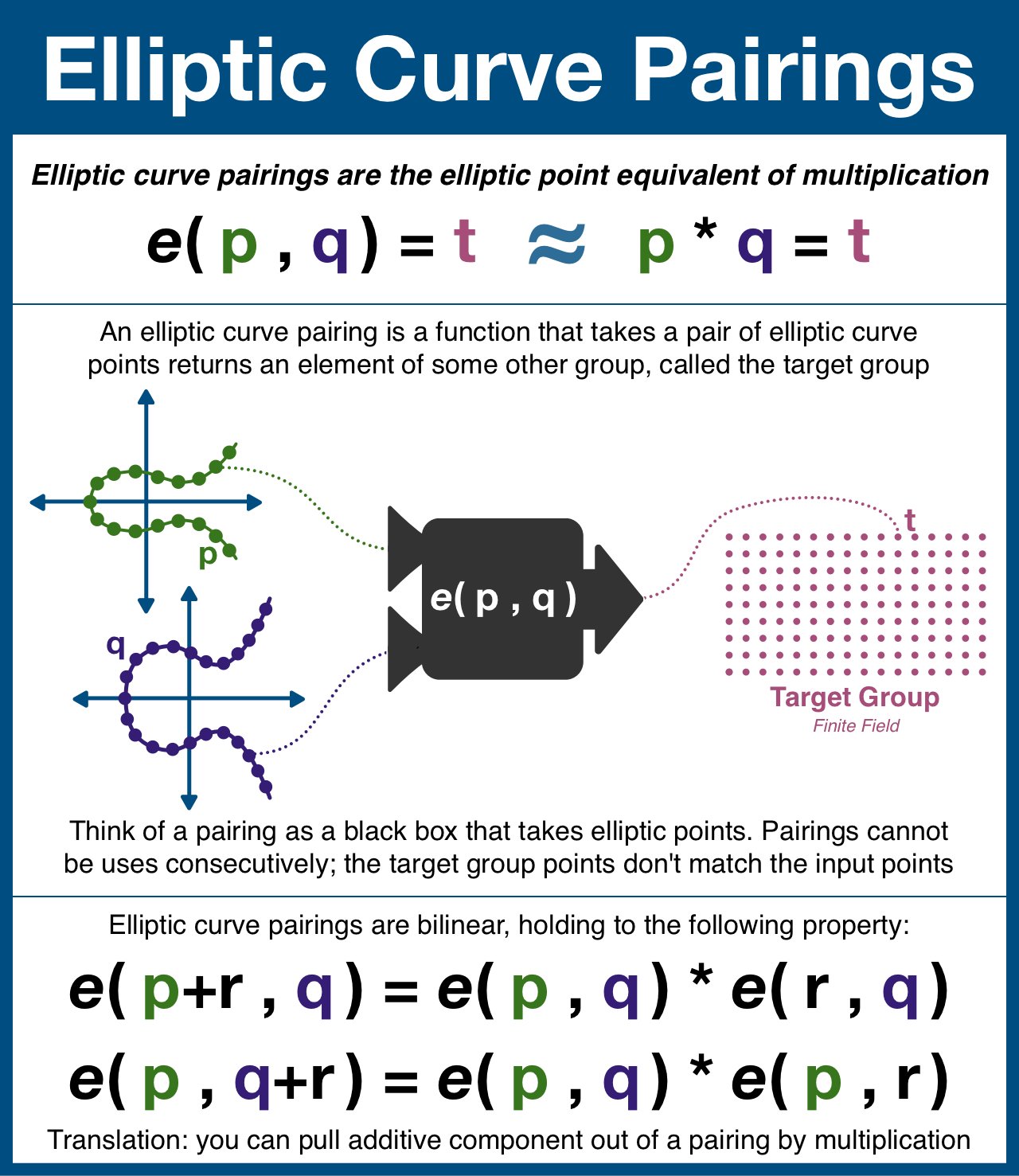
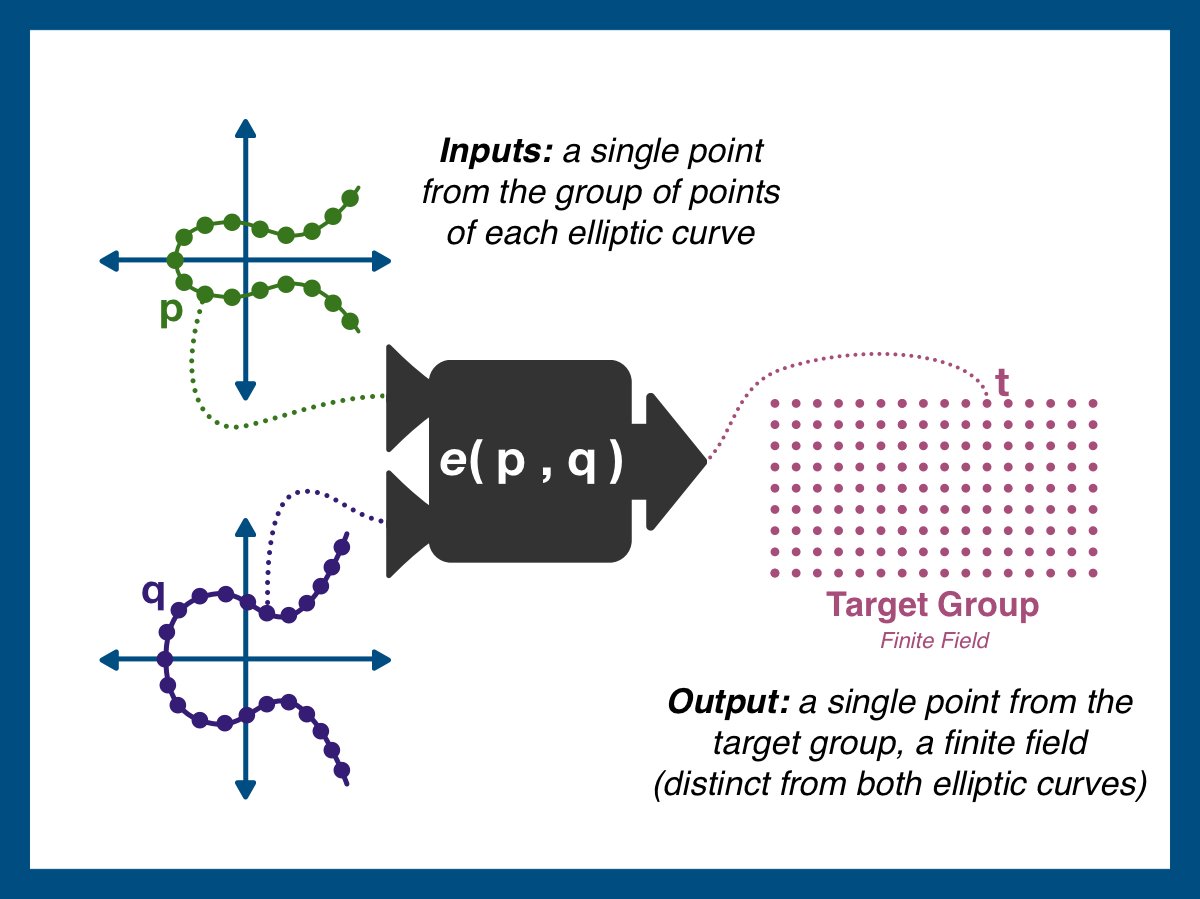
An elliptic curve pairing is a function that takes in two points on an elliptic curve and outputs a point in a finite field (think finite field = a predetermined set of points).
Think of a pairing as the elliptic curve equivalent of multiplication.
Not all elliptic curves have pairings, and not all pairings are secure. But once found, a single pairing can be shared by everyone.
Here's the plan: we are going to take two (different) elliptic curves, both of which are hiding a secret number S within their structured reference string (eg step 1 of a KZG commitment).
Once we have our two points, we will apply the pairing to get one final value.
While advanced math is difficult to visualize, the image below should help clarify.
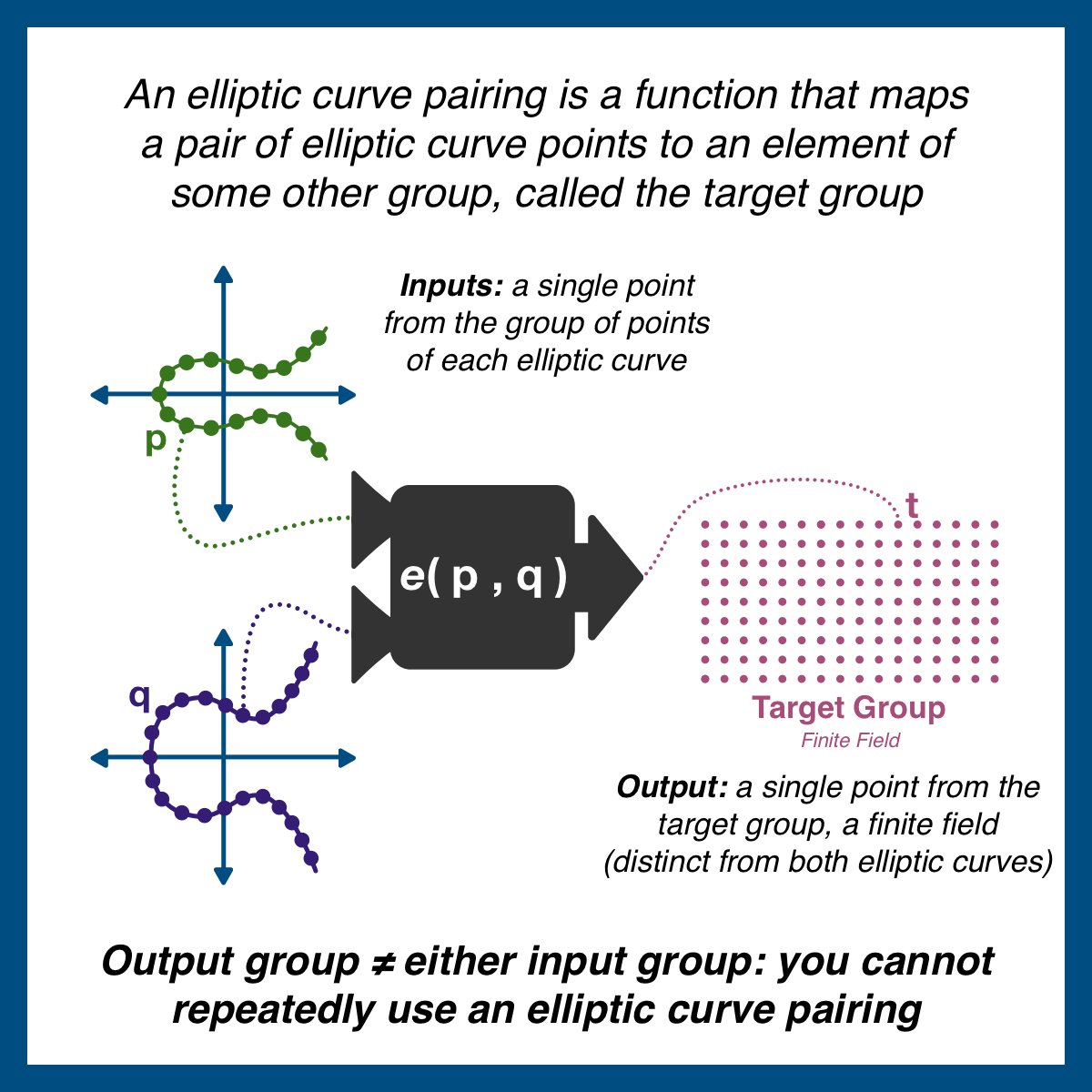
The pairing (denoted as e(p,q)) takes a point from each elliptic curve and outputs t. t is NOT a point on either curve, and therefore the pairing cannot be used more than once.
If all you care about is how we are going to use pairings, you can stop here.
We are simply going to use them like multiplication: combine two points to make a third. We will use the pairing two times with different values and compare the results, looking for equality.
¶ Properties of Pairings
The rest of this article will BRIEFLY touch on the HIGHEST levels of pairings.
Honestly, this probably wont mean anything to you unless you already know relatively advanced algebra/number theory, but it's worth including just for completeness.
¶ Bilinear
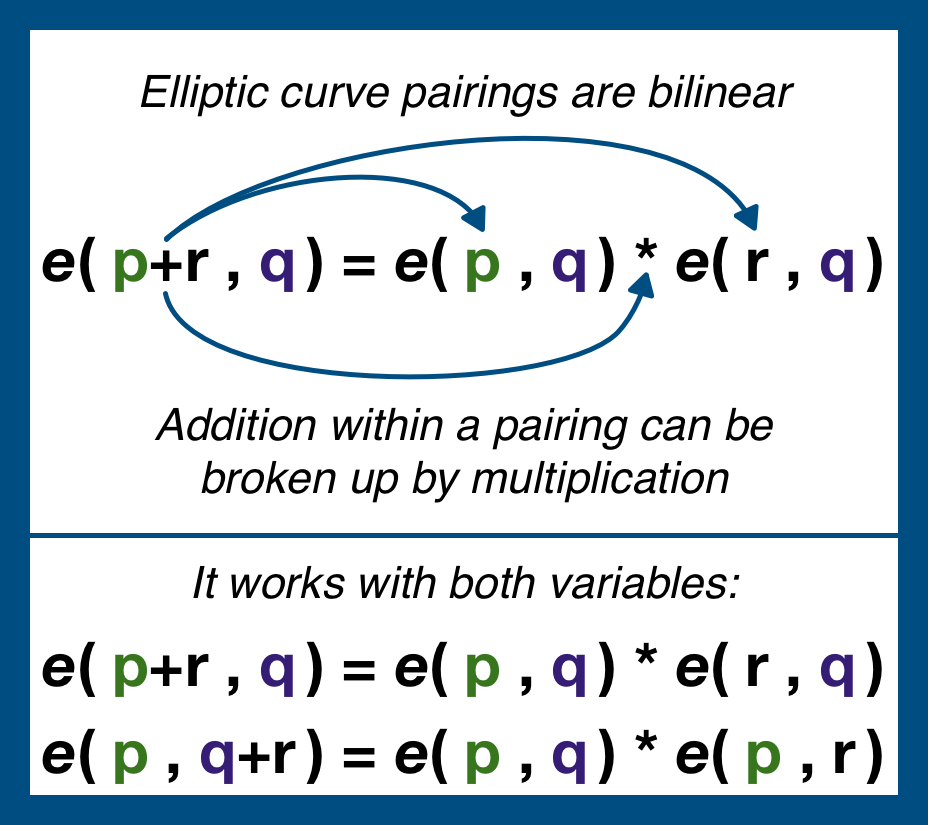
First, the most important property of pairings is that pairings are bilinear.
Bilinear is one of those arcane, hard-to-unpack terms.
Suffice to say that it is a specific algebraic property that allows us to expand/contract an expression.
¶ Diffie-Hellman
Pairings do not break 2 of the 3 properties of Diffie-Hellman:
- Still incredibly difficult:
- Discrete log problem (given gx, solve for x)
- Computational Diffie-Hellman (given gx and gy, find gxy)
- However, decision Diffie-Hellman becomes very easy.
Decision Diffie-Hellman is the property that says given gx, gy, and gz, it should be hard to to see if xy = z.
The bilinear property of elliptic pairing break this assumptions, it is trivial to test if e(gx, gy) = e(gz).
Fortunately, pairings are cyclic, meaning that as the input values grow, the output values eventually wrap back around.
And, just like all the modular arithmetic problems we work in, undoing the operation is realistically impossible.
And so, if we modify the decision Diffie-Hellman problem to a bilinear Decision Diffie-Hellman problem, pairings hold all the same properties and assumptions required to implement Diffie-Hellman and most other public cryptography schemes.
¶ Decision Linear Assumption
There is one more property of pairings that is particularly useful: the decision linear assumption (DLIN).
DLIN is incredibly abstract (it has to do with being able to distinguish the linear combination of the exponents of a generator vs a random exponent).
DLIN is a property about comparing the results of applying two matrices to the exponent (take you number n and you matrix A and create a new matrix where each matrix element is n[matrix element]).
If the rank of matrix A is less than matrix B, B will appear random vs A.
Rough idea: the target group is has more elements than either of the input groups (the target group has higher order or rank), therefore feeding inputs produces outputs that appear to be random (even if you feed them in sequential order).
¶ Summary
Bottom line: elliptic curve pairings are HARD.
This is the bleeding edge of math research... welcome to the workshop, where they make magic out of algebra!
Here is the main take away: A pairing an irreversible, one time elliptic curve point multiplication.
¶ Resources
Source Material - Twitter Link
Source Material - PDF