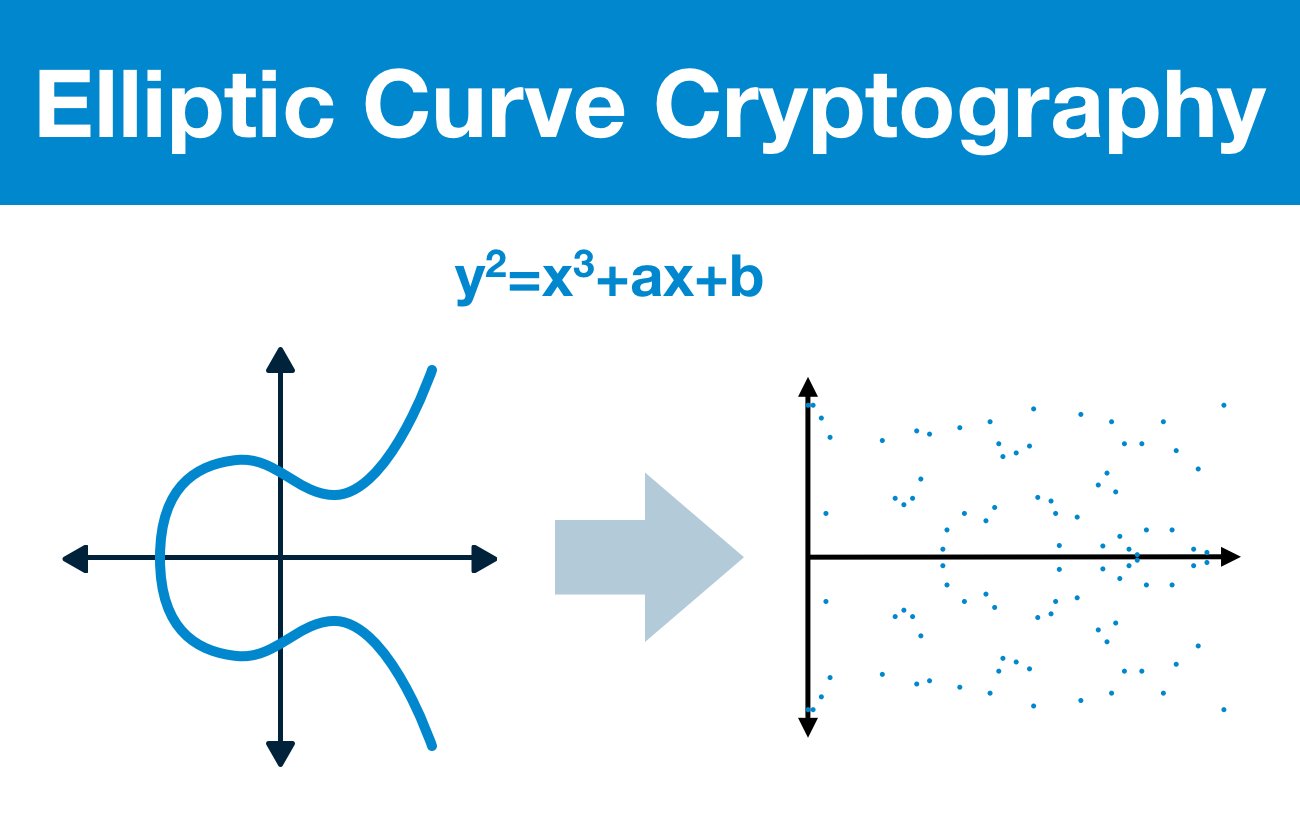
¶ Elliptic Curve Cryptography
Before we begin, a quick note. The purpose of this series is to give you a non-technical of elliptic curve cryptography and its applications for Ethereum.
There is some math, but you should be able to sail through with a high-school level education.
¶ Prerequisites
¶ Modular Arithmetic
The modulo operator (written as "mod") is the operation that finds the remainder.
- 10 / 3 = 3 with a remainder of 1 = 10 mod 3 = 1
- 14 / 6 = 2 with a remainder of 2 = 14 mod 6 = 2
- 3 / 10 = 0 with a remainder of 3 = 3 mod 10 = 3
Imagine a clock being mod 12.
¶ Building on Previous Work
In Vitalik Buterin's post on elliptic curve pairings, he warns "elliptic curves themselves are very much a nontrivial topic to understand... if you do not [know how they work], I recommend this article."
Knowing what I know now, I see why the author wrote it the way he did. No disrespect, I still refer to it often.
But I will say, I don't think it's particularly easy to take away the important things you need to learn about elliptic curves.
At least for our purposes.
So let's review the material, but this time we are going to take a different path through the same lessons. We are going to approach from a bit further out.
Let's cover the purpose of cryptography.
¶ Conversing in Public
The internet is a very public place. It basically works by blasting information at anyone listening, hoping it’ll get to its intended recipient.
The goal of cryptography is to systematically alter data until it is undecipherable and undistinguishable from random data.
Making data unreadable is easy, the trick is in altering it in a way that makes it recoverable by specific, intended recipients.
This is the problem space: how can we communicate private data through public spaces with the confidence granted by mathematical certainty?
¶ Elliptic Curves
This is an elliptic curve:
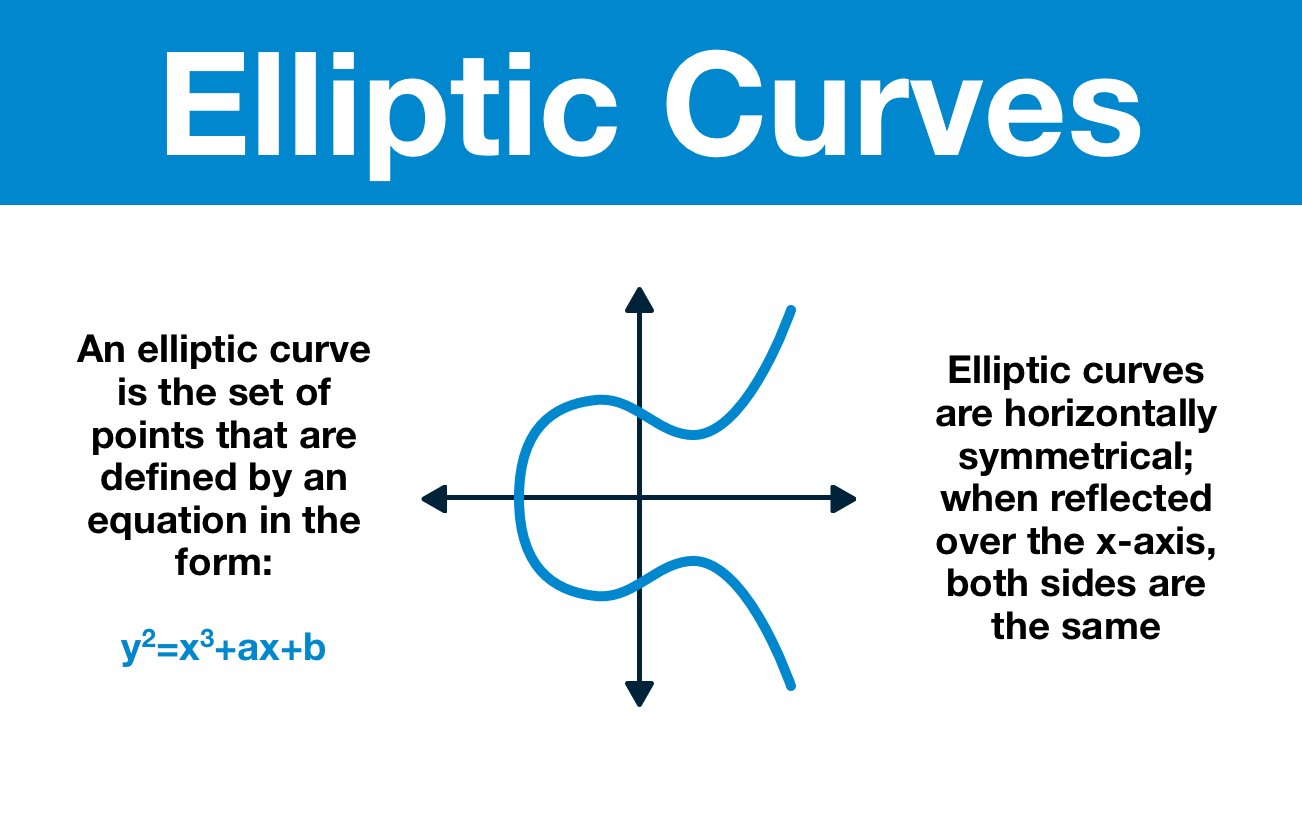
The y^2 term is particularly important. Any solution that satisfies the right side of the equation will have two y solutions: a positive and a negative.
If y = 3 is a solution, so is y = -3; both are equally correct.
Squaring y introduces ambiguity.
¶ Secret Numbers
Let's say there's a secret number y that we both know, but we aren't sure if the other person knows. The goal is to figure out if the other person knows without giving up the secret.
We can leverage the ambiguity in our elliptic curve equation.
Instead of sharing y (or any info that could be used to derive y), we could agree upon an elliptic curve equation and agree to share the x value that corresponds with our y.
That x could reference y or -y; it is ambiguous.
If we stopped here, we would be able to support just this 50/50 type of ambiguity. This can be useful; a lot of critical info is binary.
But we are not going to stop here.
We are going to add more ambiguity until we can use it to obscure something substantial.
¶ Diffie–Hellman Key Exchange
Deep Dive: Diffie–Hellman Key Exchange
The best place to start is always with the solutions that came before.
Diffie-Hellman works by generated a shared secret by passing intermediate, non-sensitive messages through public spaces.
These intermediate messages contain sensitive data, but they protect the value by looping through modular arithmetic.
You can see the final result, but you have no idea how many times the result passed through the mod operator before it got there.
¶ Manipulating Elliptic Curve Points
Our first goal is going to be to move this dynamic to elliptic curves. In order to do so, two things need to be possible:
- we can conduct the mathematical operations needed to move between points
- these operations still work when we apply modular arithmetic
This is one of those moments where I think the previous telling was not particularly useful.
It just defined this bizarre operation, and called it a dot operation and then kinda just... moved on...
Here's what you actually need to know about dot operations: they exist.
What's practically useful is understanding that the dot operation is the elliptic curve-version of addition. You can dot/add two separate points to get a third, it's just the visualization that's weird.
We can dot/add two points and we can dot/add a point to itself.
From this primitive, we can build all the tools needed to execute the math needed to create the ambiguity of Diffie-Hellman.
¶ Elliptic Curve Discrete Logarithm
And for the sake of time (and sanity) I'll just cut to the chase: everything works just as well in modular arithmetic too.
So then the question becomes "how do we apply modular arithmetic to a curve?"
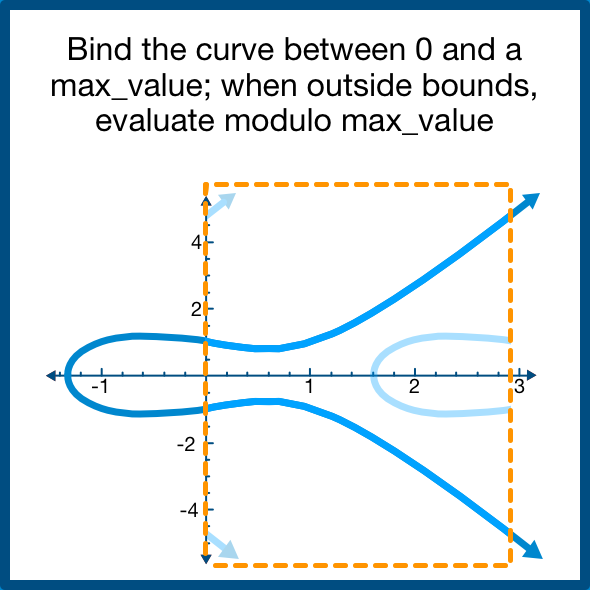
It's not too bad, you just wrap the graph back within a boundary. Once you're done, you have two layers of ambiguity:
- y2
- mod max_value
We have reached the impenetrable foundation of elliptic curve cartography: the elliptic curve discrete logarithm problem.
The discrete logarithm problem (factoring modular numbers) is provably difficult, the extra layer of ambiguity makes it SIGNIFICANTLY more difficult.
For Reference:

¶ Finite Field Generation
At this stage we are done! We now have all the fundamentals we need to continue on our journey to understanding how Ethereum leverages elliptic curve cryptography. But, for the sake of completeness (and to save time later), let's include the finite field generation.
At this point it's very simple: we just take our elliptic curve in modular space and throw out all the values where x is not a whole number.
This constrains the elliptic curve to only apply to x-value integers, which will become useful a little bit down the line.
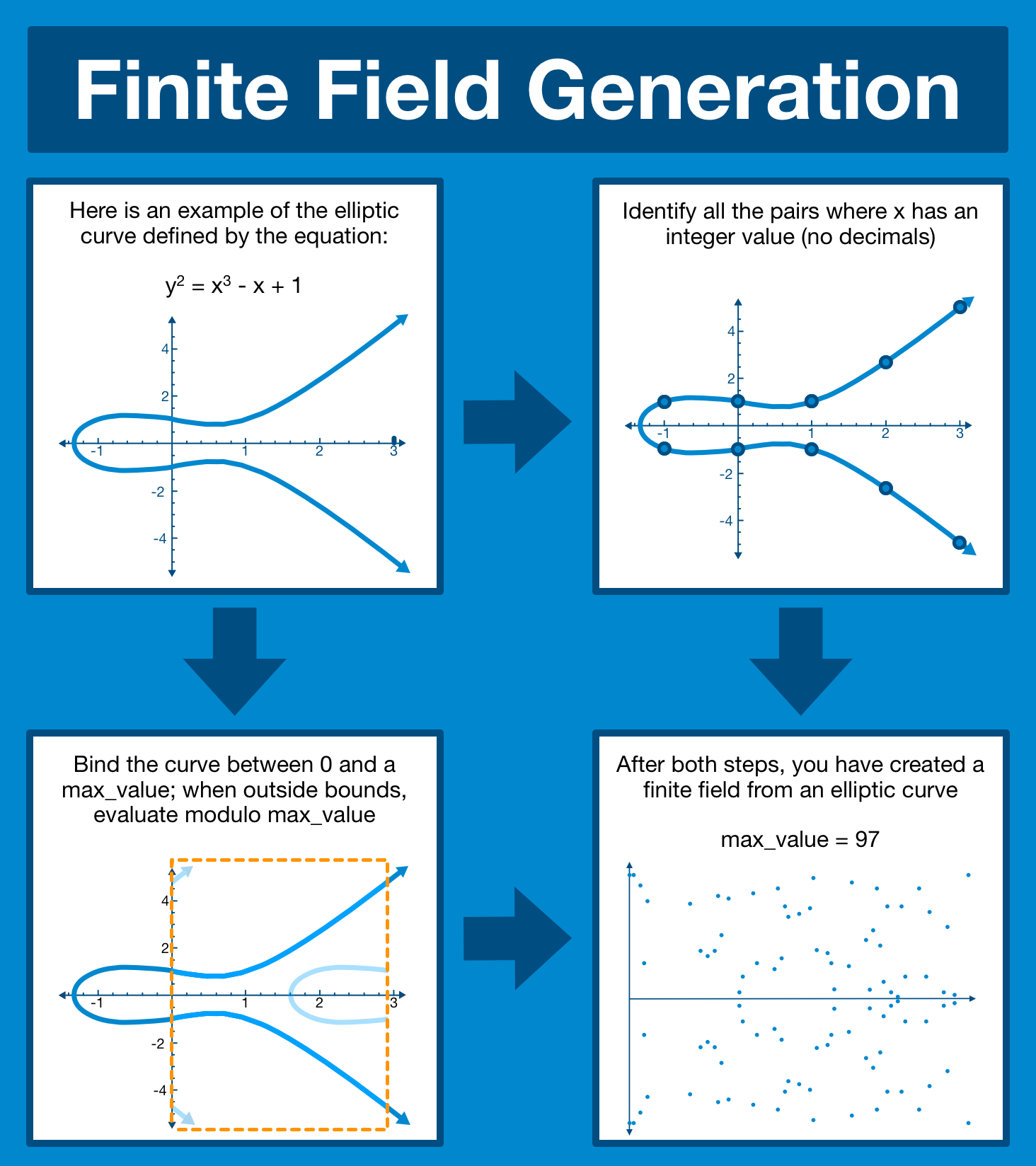
And so here's where we will part, with a finite field generated from an elliptic curve.
When you look at it on it's own, it really seems to look like a random jumble of numbers, especially if you weren't around when we built it...
I wonder how that could come in handy?
¶ Resources
This article combines the work of 2 tweet threads:
- A Practical Guide to Elliptic Curve Cryptography
- Source Material - Twitter Link
- Source Material - PDF
- Elliptic Curve Cryptography
- Source Material - Twitter Link
- Source Material - PDF