
Turing Machines and Turing-Completeness
To understand The World Computer you have to understand the Proto-Computer: The Turing Machine.
Invented by Alan Turing in the 1930s who named it an "A-machine," a Turing machine is an (abstract) model of computation.
Turing-Machine
The concept is built around a simple hypothetical machine. It contains 3 key components:
- The tape, representing memory
- The head, keeping track of the machine position
- The instructions, telling the machine how to process the data.
The instructions are a set of conditions and associated operations. There are 3 possible operations:
- Read the symbol under the head
- Edit (write and/or erase) the symbol under the head
- Move left or right one square
A Simple Example
A Turing machine might look like this. While we are going to stick to 0s and 1s, a Turing machine can process any letters, numbers or symbols.
Head, Tape & Instructions
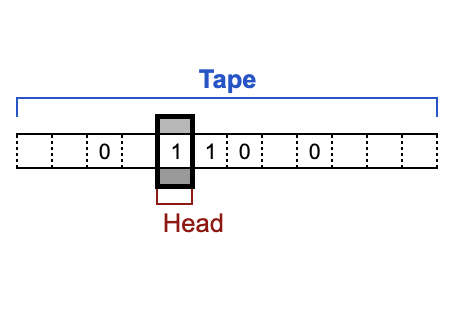
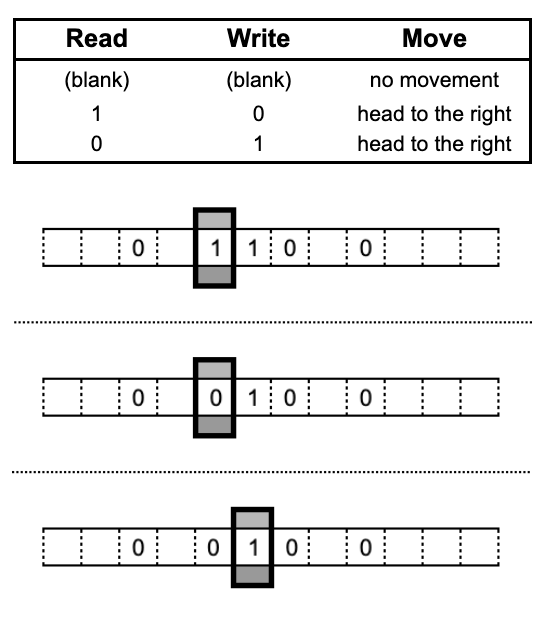
Our goal is to switch the 1s to 0s and vice versa. Let's construct a set of steps to achieve this flip:
- Read the tape and see if it is 1 or a 0
- Write the new symbol
- Move to the next number
Congratulations! We've created our first instruction.
Machine State
If we run our instruction two more times, we'll find ourselves at a blank space. Our Turing machine will follow our instruction and wait endlessly.
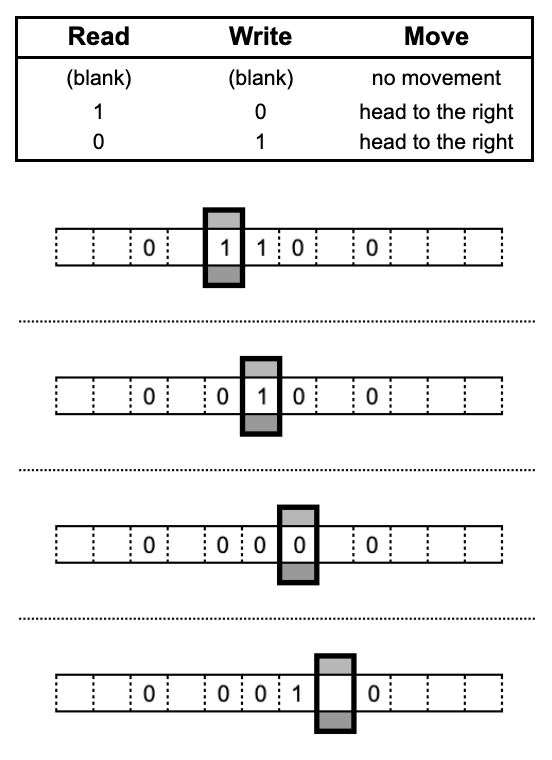
At this point we have to introduce the final concept required for a Turning machine: the machine state. The machine state is an additional field the Turing machine uses that allows it to take different actions based on previous actions.
Now that the Turing machine can understand state, it can make decisions based on the context of the data on the tape.
Implementing Inversion
In the example above, we introduced a state that instructs the machine to halt; but we can use the concept to begin to implement more complex functionality.
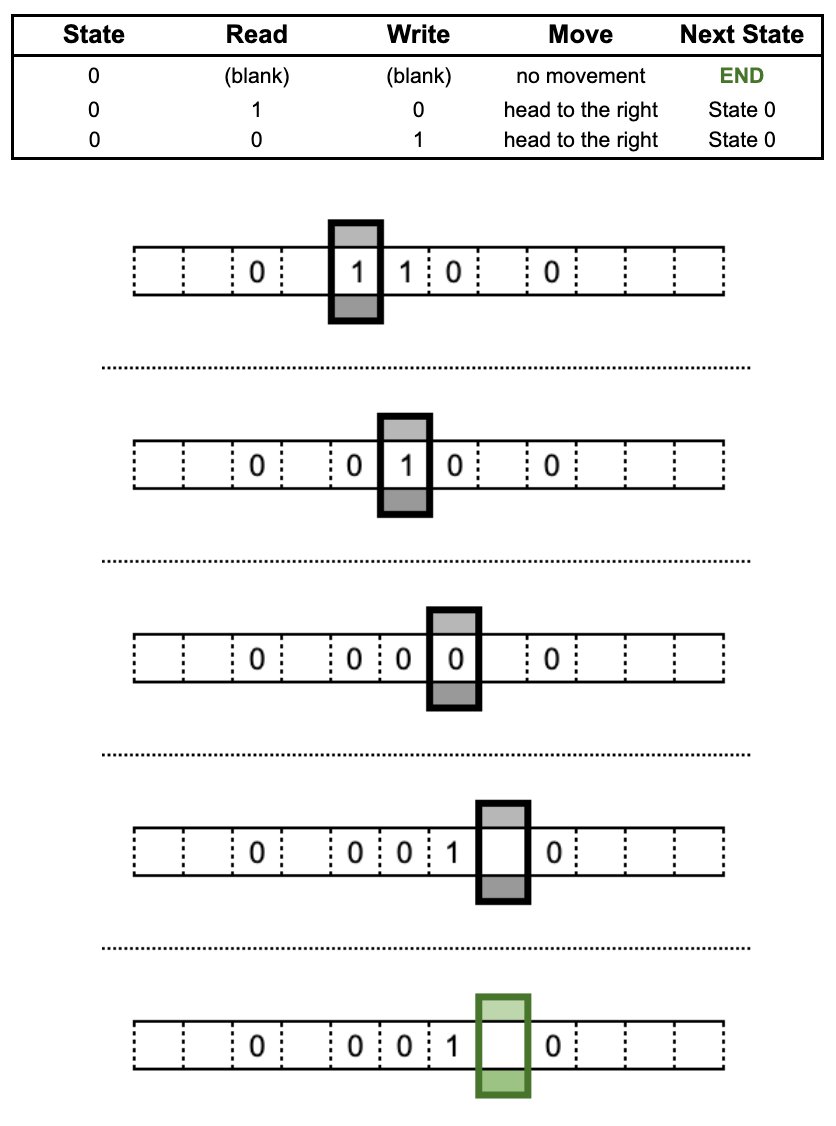
Consider this Turing Machine instruction set.
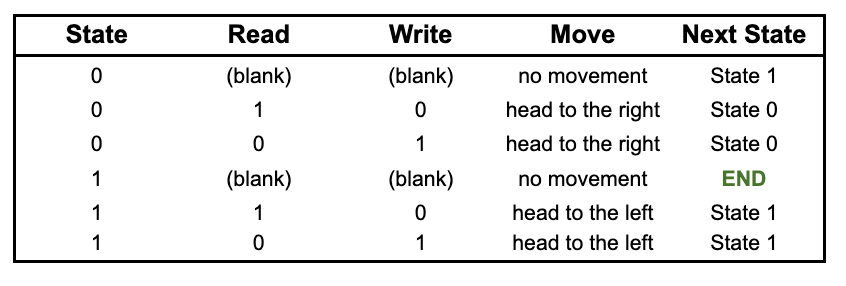
In state 0, the head moves right inverting each symbol.
When it reaches an empty space, it will move to state 1.
In state 1, the head moves left and once again inverts the symbols.
At an empty space the program ends.
Turing-Completeness
This the end of our example, which is a little silly. All it does it invert the number back and forth, ending in the original state. But with the introduction of more states to our program, we can instruct the Turing machine to perform more complex functions.
In fact, with enough states and a detailed enough instruction set, a Turing machine is capable of ANY computation a modern computer can do.
Take a look at your Macbook. If you can do something on that computer, you can (theoretically) do it on a Turing machine.
In computability theory, Turing-completeness is a designation that describes a system with formal and specific requirements. For now we are going to keep things high level. Let's use this definition:
A system is Turing-Complete if it can simulate a Turing machine.
Over the last century, Turing, Church and the giants who've built on their work have mathematically proven that if you can simulate a Turing machine on a computational system, you can also simulate that system on a Turing machine.
Put simply, if a system is Turing-complete it is capable of anything that any other Turing-complete system can do.
Ethereum and Turing-Completeness
Here are two pieces of information:
- most modern programming languages are Turing-complete
- Solidity is Turing-complete
Turing-completeness allows us to say with mathematical certainty that Ethereum is capable of anything that your computer can do.
Ethereum is the World Computer, crypto is programmable money, De-Fi is possible...
...because solidity is Turing-complete!
I can already hear the peanut gallery:
- "30 transactions per second???"
- "Have you seen gas fees???"
- "Have you tried [other blockchain]???"
Go back and ask Dr. Turing what his contemporaries said about computing. I bet he'd have the same answer: "We are still building."
A new type of computer is being born.
Resources
Source Material - Tweet Link